题目内容
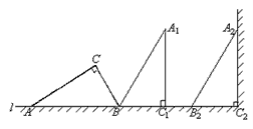
【题目】如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在L上),最后沿BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边)。
(1)求出AB的长;
(2)求出AC的长;
(3)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
【答案】(1) AB=2米; (2)AC=![]() 米;(3)画图见解析;
米;(3)画图见解析;![]() .
.
【解析】
试题(1)(2)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(3)根据要求画出路径,再用弧长公式求解路径的长度.根据题意得到Rt△ABC在直线l上转动两次点A分别绕点B旋转120°和绕C旋转90°,将两条弧长求出来加在一起即可.
试题解析:(1)(2)∵∠CAB=30°,BC=1米
∴AB=2米,AC=![]() 米.
米.
(3)画出A点经过的路径:
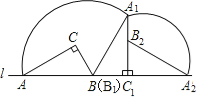
∵∠ABA1=180°-60°=120°,A1A2=AC=![]() 米
米
∴A点所经过的路径长=![]() (米).
(米).
(3)在Rt△ABC中,∵BC=1,AC=![]()
∴AB=2,∠CBA=60°,
∴![]() ,
,![]() ,
,
∴点A经过的路线的长是![]() .
.
故两次翻转此物的整个过程点A经过路径的长度为是![]() .
.
考点: 1.弧长的计算;2.旋转的性质;3.解直角三角形.

练习册系列答案
相关题目