��Ŀ����
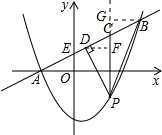
��ͼ����ƽ��ֱ������ϵ�У�ֱ�� ��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��1���������ߵĽ���ʽ��
��2�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ��Ƿ�����ʺϵ�m��ֵ��ʹ�����������ε������Ϊ1:2�������ڣ�ֱ��д��m��ֵ���������ڣ���˵�����ɣ�

 ��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D����1���������ߵĽ���ʽ��
��2�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ��Ƿ�����ʺϵ�m��ֵ��ʹ�����������ε������Ϊ1:2�������ڣ�ֱ��д��m��ֵ���������ڣ���˵�����ɣ�

��1��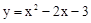 ����2����
����2���� ��
��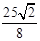 ����0��3.
����0��3.
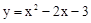 ����2����
����2���� ��
��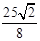 ����0��3.
����0��3.�����������1����y=x+1�У���y=0ʱ��x=-1����y=5ʱ��x=4�����˿ɵ�A��B�����ꣻ��A��B������������߽���ʽ���a��b��ֵ������ȷ���������߽���ʽ��
��2������ֱ��AB��y�ύ�ڵ�E����CP��y��ƽ�У��õ���ACP=��AEO�����AE��OA�ij����ó�sin��AEO��ֵ����Ϊsin��ACP��ֵ����P�ĺ�����Ϊm���ֱ����ֱ���������߽���ʽ�õ�����������֮��ΪPC�ij�����PD=PCsin��ACP��ʾ��PD�����ö��κ������������PD�����ֵ���ɣ�
�ڴ��ڣ���D��DF��CP����B��BG��PQ����PC�ӳ������Q����ʾ��DF��BG��������ʾ��������DCP�����������BCP������������֮��Ϊ1��2�г�����m�ķ��̣�������̵Ľ�õ�m��ֵ���ɣ�
�����������1����
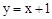 �У���y=0ʱ��x=-1����y=5ʱ��x=4��
�У���y=0ʱ��x=-1����y=5ʱ��x=4����A(-1��0)��B(4��5) .
��A(-1��0)��B(4��5)�ֱ����y��ax2��bx��3�У���
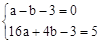 �����
�����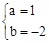 ��
�����������ʽΪ
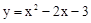 .
.��2������ֱ��AB��y���ڵ�E�����E��0��1������OA=OE����AEO=45��,��ACP=��AEO="45��,"
��
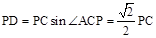 ��
�� ��
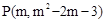 ����
����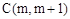 ��
����
 ��
����
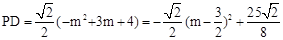 ��
����PD�����ֵΪ
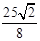 ��
���ڵ�m=0��m=3ʱ��PC�ѡ�PDB�ֳ����������ε������Ϊ1:2��
��ͼ����D��DF��CP����B��BG��PQ����PC�ӳ������Q��
��sin��ACP=
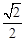 ����cos��ACP=
����cos��ACP=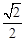 .
.��Rt��PDF�У�DF=DP•sin��DPC=DP•cos��ACP=
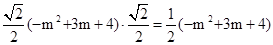 .
.�֡�BG=4-m��
��
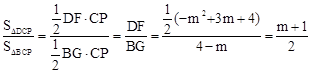 .
.��
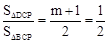 ʱ����ã�m=0��
ʱ����ã�m=0����
 2ʱ����ã�m=3��
2ʱ����ã�m=3���ʵ�m=0��m=3ʱ��PC�ѡ�PDB�ֳ����������ε������Ϊ1��2��

��ϰ��ϵ�д�
�����Ŀ
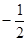 x2+bx+c���㣨-6,-2������y�ύ�ڵ�C���ҶԳ�����x�ύ�ڵ�B��-2,0��������ΪA.
x2+bx+c���㣨-6,-2������y�ύ�ڵ�C���ҶԳ�����x�ύ�ڵ�B��-2,0��������ΪA.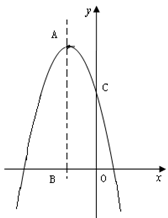
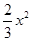 ��ͼ����ͼ����A0λ������ԭ�㣬��A1��A2��A3��An��y����������ϣ���B1��B2��B3��Bn�ڶ��κ���λ�ڵ�һ����ͼ���ϣ���C1��C2��C3��Cn�ڶ��κ���λ�ڵڶ�����ͼ���ϣ��ı���A0B1A1C1���ı���A1B2A2C2���ı���A2B3A3C3���ı���An��1BnAnCn�������Σ���A0B1A1=��A1B2A1=��A2B3A3��=��An1BnAn
��ͼ����ͼ����A0λ������ԭ�㣬��A1��A2��A3��An��y����������ϣ���B1��B2��B3��Bn�ڶ��κ���λ�ڵ�һ����ͼ���ϣ���C1��C2��C3��Cn�ڶ��κ���λ�ڵڶ�����ͼ���ϣ��ı���A0B1A1C1���ı���A1B2A2C2���ı���A2B3A3C3���ı���An��1BnAnCn�������Σ���A0B1A1=��A1B2A1=��A2B3A3��=��An1BnAn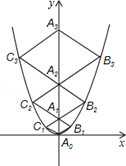
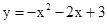 ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���. DQ�����F������.
DQ�����F������.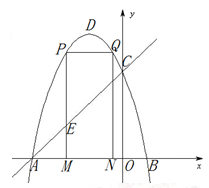
 �������ڵ�C����
�������ڵ�C����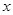 �ύ��A��B���㣬��ACD=90�㣬������
�ύ��A��B���㣬��ACD=90�㣬������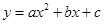 ����A��B��C���㣮
����A��B��C���㣮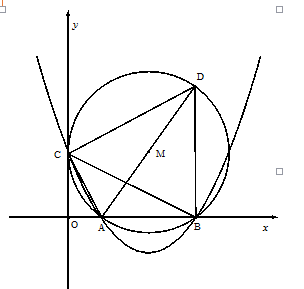
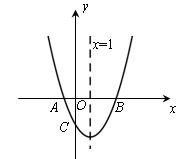
 ������������
������������ ƽ�Ƶõ�,������ƽ�ƹ�����ȷ����
ƽ�Ƶõ�,������ƽ�ƹ�����ȷ����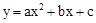 �У�����y��x�IJ��ֶ�Ӧֵ���£�
�У�����y��x�IJ��ֶ�Ӧֵ���£�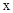
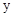
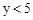 ʱ��x��ȡֵ��Χ�� .
ʱ��x��ȡֵ��Χ�� .