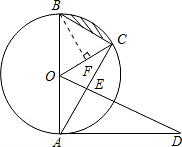
题目内容
如图,AB是⊙O的直径,AD与⊙O相切于点A,过B点作BC∥OD交⊙O于点C,连接OC、AC,AC交OD于点E.
(1)求证:△COE∽△ABC;
(2)若AB=2,AD=
,求图中阴影部分的面积.

(1)求证:△COE∽△ABC;
(2)若AB=2,AD=
| 3 |

(1)证明:∵AB为⊙O的直径,
∴∠BCA=90°,
又∵BC∥OD,
∴OE⊥AC,
即:∠OEC=∠BCA=90°.(2分)
又∵OA=OC,
∴∠BAC=∠OCE,(3分)
∴△COE∽△ABC;(4分)
(2)过点B作BF⊥OC,垂足为F.
∵AD与⊙O相切,
∴∠OAD=90°,
在Rt△OAD中,
∵OA=1,AD=
,
∴tan∠D=
,
∴∠D=30°,(5分)
又∵∠BAC+∠EAD=∠D+∠EAD=90°,
∴∠BAC=∠D=30°,
∠BOC=60°,(6分)
∴S△OBC=
•OC•BF=
×1×1×sin60°=
,(7分)
∴S阴=S扇OCB-S△OBC=
-
=
-
.(8分)
∴∠BCA=90°,
又∵BC∥OD,
∴OE⊥AC,
即:∠OEC=∠BCA=90°.(2分)
又∵OA=OC,
∴∠BAC=∠OCE,(3分)
∴△COE∽△ABC;(4分)
(2)过点B作BF⊥OC,垂足为F.
∵AD与⊙O相切,
∴∠OAD=90°,
在Rt△OAD中,
∵OA=1,AD=
| 3 |
∴tan∠D=
| ||
| 3 |
∴∠D=30°,(5分)
又∵∠BAC+∠EAD=∠D+∠EAD=90°,
∴∠BAC=∠D=30°,
∠BOC=60°,(6分)
∴S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴S阴=S扇OCB-S△OBC=
| 60π×12 |
| 360 |
| ||
| 4 |
| π |
| 6 |
| ||
| 4 |


练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目




 (π取3.14).
(π取3.14).



