题目内容
已知△ABC三边长a、b、c,且满足(a-2)2+|b-2|+|c-2
|=0,则此三角形一定是( )
| 2 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
分析:根据平方,绝对值相加为0,可分别求出a,b,c的值,根据边长可判断三角形的形状.
解答:解:∵(a-2)2+|b-2|+|c-2
|=0,
∴a-2=0,a=2;b-2=0,b=2;c-2
=0,c=2
.
∵22+22=(2
)2,
即:a2+b2=c2,
∴所以此三角形是直角三角形.
又∵a=b,
∴故此三角形是等腰直角三角形.
故选C.
| 2 |
∴a-2=0,a=2;b-2=0,b=2;c-2
| 2 |
| 2 |
∵22+22=(2
| 2 |
即:a2+b2=c2,
∴所以此三角形是直角三角形.
又∵a=b,
∴故此三角形是等腰直角三角形.
故选C.
点评:本题考查勾股定理的逆定理,非负数的性质-绝对值和偶次方,求出a,b,c的值,根据边长判断三角形的形状.

练习册系列答案
相关题目
已知△ABC三边长分别为4,4,4
,则△ABC的面积为( )
| 2 |
| A、6 | B、8 | C、10 | D、12 |
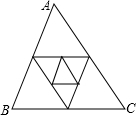 如图,已知△ABC三边长为a、b、c,三条中位线组成一个新的三角形,新的三角形的中位线又组成一个三角形,以此类推,第五次组成的三角形的周长为
如图,已知△ABC三边长为a、b、c,三条中位线组成一个新的三角形,新的三角形的中位线又组成一个三角形,以此类推,第五次组成的三角形的周长为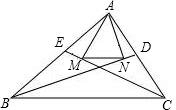 如图,自△ABC顶点A向∠C与∠B的角平分线CE、BD作垂线AM、AN,垂足分别是M、N,已知△ABC三边长为a、b、c,则MN=
如图,自△ABC顶点A向∠C与∠B的角平分线CE、BD作垂线AM、AN,垂足分别是M、N,已知△ABC三边长为a、b、c,则MN=