题目内容
如图，自△ABC顶点A向∠C与∠B的角平分线CE、BD作垂线AM、AN，垂足分别是M、N，已知△ABC三边长为a、b、c，则MN=分析：延长AM、AN交BC于F、G．根据ASA发现两对全等三角形，根据全等三角形的性质得到MN是三角形AFG的中位线，同时得到FG的长，根据三角形的中位线定理即可计算．
解答：
解：延长AM、AN交BC于F、G．
∵∠ACM=∠FCM，CM=CM，∠AMC=∠FMC，
∴△ACM≌△FCM，
∴AM=FM，CF=AC．
同理AN=NG，BG=AB．
∴MN=
FG=
．
故答案为：
．
解：延长AM、AN交BC于F、G．∵∠ACM=∠FCM，CM=CM，∠AMC=∠FMC，
∴△ACM≌△FCM，
∴AM=FM，CF=AC．
同理AN=NG，BG=AB．
∴MN=
| 1 |
| 2 |
| b+c-a |
| 2 |
故答案为：
| b+c-a |
| 2 |
点评：此题综合考查了全等三角形的判定和性质、三角形的中位线定理．
练习册系列答案
相关题目
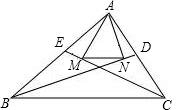如图，自△ABC顶点A向∠C与∠B的角平分线CE、BD作垂线AM、AN，垂足分别是M、N，已知△ABC三边长为a、b、c，则MN=________．
