Question

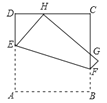
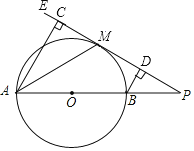
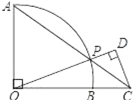
【题目】如图，O为所在圆的圆心，∠AOB＝90°，点P在上运动（不与点A，B重合），AP交OB延长线于点C，CD⊥OP于点D．若OB＝2BC＝2，则PD的长是（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

通过证明△OAC∽△DPC，可得，可设PD=2x，CD=3x，由勾股定理，可求x的值，即可求解．

∵OB=2BC=2，

∴BC=1，OA=OP=2，OC=OB+BC=3，

∵OA=OP，

∴∠OAC=∠OPA，

∵∠OPA=∠CPD，

∴∠OAC=∠CPD，且∠D=∠AOC=90°，

∴△OAC∽△DPC，

∴，

∴设，，

∵CD2+OD2=OC2，

∴9x2+(2+2x)2=9，

∴x1=，x2=﹣1(不合题意舍去)，

∴PD=2x=，

故选：B．