题目内容
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF .
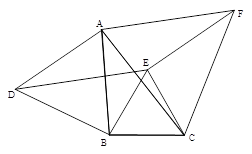
(1)将△CBA绕着点C旋转,可以与哪一个三角形重合,以及旋转的度数(直接写答案);
(2)四边形AFED一定是平行四边形吗?如果是,请说明理由;
(3)当△ABC满足什么条件时,四边形AFED一定是菱形.( 直接写答案,不必说明理由)

(1)将△CBA绕着点C旋转,可以与哪一个三角形重合,以及旋转的度数(直接写答案);
(2)四边形AFED一定是平行四边形吗?如果是,请说明理由;
(3)当△ABC满足什么条件时,四边形AFED一定是菱形.( 直接写答案,不必说明理由)
(1)△CEF, 顺时针60o(2) 是,理由见解析(3)AB=AC
(1)△CEF, 顺时针60o …………2分
(2) 四边形AFED是平行四边形 …………3分
∵△ABD、△BCE、△ACF为等边三角形
∴CB="CE,CA=CF," ∠BCE=∠ACF=60o
∴∠BCE-∠ACE=∠ACF-∠ACE即∠BCA=∠ECF
∴△ABC≌△FEC
∴AB=EF …………5分
又∵AB=AD ∴AD=FE
同理可证△ABC≌△DBE,BD=FA
∴四边形AFED是平行四边形 …………7分
(3)AB=AC …………8分
(1)根据等边三角形BEC和ACF,推出AC=CF,BC=CE,∠ECB=∠FCA=60°,求出∠ACB=∠FCE,根据SAS证△ABC和△FEC全等即可;
(2)由(1)推出AD=FE,同理求出△ABC≌DBE,推出BD=AF,根据平行四边形的判定推出即可;
(3)根据AB=AC和AB=EF,AC=AF,推出AD=DE=EF=AF,根据菱形的判定即可推出四边形AFED是菱形.
(2) 四边形AFED是平行四边形 …………3分
∵△ABD、△BCE、△ACF为等边三角形
∴CB="CE,CA=CF," ∠BCE=∠ACF=60o
∴∠BCE-∠ACE=∠ACF-∠ACE即∠BCA=∠ECF
∴△ABC≌△FEC
∴AB=EF …………5分
又∵AB=AD ∴AD=FE
同理可证△ABC≌△DBE,BD=FA
∴四边形AFED是平行四边形 …………7分
(3)AB=AC …………8分
(1)根据等边三角形BEC和ACF,推出AC=CF,BC=CE,∠ECB=∠FCA=60°,求出∠ACB=∠FCE,根据SAS证△ABC和△FEC全等即可;
(2)由(1)推出AD=FE,同理求出△ABC≌DBE,推出BD=AF,根据平行四边形的判定推出即可;
(3)根据AB=AC和AB=EF,AC=AF,推出AD=DE=EF=AF,根据菱形的判定即可推出四边形AFED是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
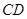 是由线段
是由线段 平移得到的,且点
平移得到的,且点 (-1,3)的对应点为
(-1,3)的对应点为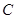 (2,5),那么点
(2,5),那么点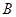 (-3,-1)的对应点
(-3,-1)的对应点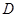 的坐标是 .
的坐标是 .
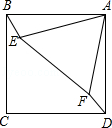
 为折痕,则
为折痕,则 的度数为______.
的度数为______.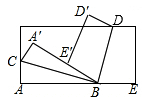

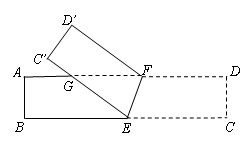
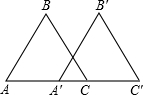
 ABC沿射线AC方向平移2 cm得到,若AC=3cm,则A’C
ABC沿射线AC方向平移2 cm得到,若AC=3cm,则A’C