题目内容
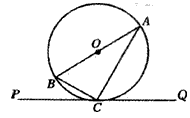
如下图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F。

①请向AB与AC的大小有什么关系?为什么?
②按角的大小分类,请你判断△ABC是哪一类的三角形,请说明理由。
(1)AB=AC
理由为:连接AD
∵AB是⊙O的直径
∴∠ADB=90°,即:AD⊥BC
∵BD=CD
∴AD是三角形BAC中BC边的垂直平分线
∴AB=AC
(2)三角形ABC属于锐角三角形
理由为:AC交⊙O于F,点F不与点A重合
连接BF,则∠BFA<90°
所以,∠BAC<90° …
显然,∠B=∠C<∠ADC=90°
所以,三角形ABC属于锐角三角形

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目


 AC ④DE是⊙O的切线
AC ④DE是⊙O的切线