题目内容
如下图，AB是⊙O的直径，直线PQ是⊙O的切线，C是切点。求证：∠BCP=∠A。
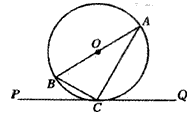
证明：连接OC，则OB=OC，
∴∠B=∠OCB。
∵直线PQ是⊙O的切线，C是切点，
∴OC⊥PQ，
∴∠BCP+∠OCB=90°
∴∠BCP+∠B=90°
又∵AB是⊙O的直径，
∴∠ACB=90°
∴∠A+∠B=90°，
∴∠BCP=∠A
∴∠B=∠OCB。
∵直线PQ是⊙O的切线，C是切点，
∴OC⊥PQ，
∴∠BCP+∠OCB=90°
∴∠BCP+∠B=90°
又∵AB是⊙O的直径，
∴∠ACB=90°
∴∠A+∠B=90°，
∴∠BCP=∠A
练习册系列答案
阅读快车系列答案
相关题目
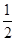AC ④DE是⊙O的切线
