题目内容
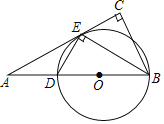
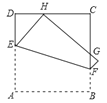
【题目】如图，将正方形ABCD折叠，使点A与CD边上的点H重合（H不与C，D重合），折痕交AD于点E，交BC于点F，边AB折叠后与边BC交于点G．设正方形ABCD周长为m，△CHG周长为n，则
的值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
由题意连接AH、AG，作AM⊥HG于M．利用正方形的性质以及全等三角形的判定与性质进行等量替换从而求出
的值.
解：连接AH、AG，作AM⊥HG于M．
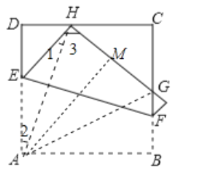
∵四边形ABCD是正方形，
∴AD=AB．
∴AM=AB．
∵EA=EH，
∴∠1=∠2，
∵∠EAB=∠EHG=90°，
∴∠HAB=∠AHG，
∵DH∥AB，
∴∠DHA=∠HAB=∠AHM，
∵AH=AH，∠D=∠AMH=90°，
∴△AHD≌△AHM，
∴DH=HM，AD=AM，
∵AM=AB，AG=AG，
∴Rt△AGM≌Rt△AGB，
∴GM=GB，
∴△GCH的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC，
∵四边形ABCD的周长=m=4BC，
∴
.
故选：B.
练习册系列答案
相关题目
