题目内容
如图所示,在平面直角坐标系中有点A(-1,0),点B(4,0),以AB为直径的半圆交y轴正半轴于点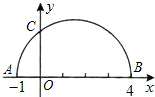 C.
C.
(1)求点C的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)在(2)的条件下,若在抛物线上有一点D,使四边形BOCD为直角梯形,求直线BD的解析式;
(4)设点M是抛物线上任意一点,过点M作MN⊥y轴,交y轴于点N.若在线段AB上有且只有一点P,使∠MPN为直角,求点M的坐标.
 C.
C.(1)求点C的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)在(2)的条件下,若在抛物线上有一点D,使四边形BOCD为直角梯形,求直线BD的解析式;
(4)设点M是抛物线上任意一点,过点M作MN⊥y轴,交y轴于点N.若在线段AB上有且只有一点P,使∠MPN为直角,求点M的坐标.
(1)C点的坐标为(0,2);理由如下:
如图,连接AC,CB.依相交弦定理的推论可得OC2=OA•OB,
解得OC=2.
故C点的坐标为(0,2).
(2)设抛物线解析式为y=a(x+1)(x-4).
把点C(0,2)的坐标代入上式得a=-
.
∴抛物线解析式是y=-
x2+
x+2.
(3)如图,过点C作CD∥OB,交抛物线于点D,则四边形BOCD为直角梯形.
由(2)知抛物线的对称轴是x=
,
∴点D的坐标为(3,2).
设过点B,点D的解析式是y=kx+b.
把点B(4,0),点D(3,2)的坐标代入上式得
解之得
∴直线BD的解析式是y=-2x+8.
(4)依题意可知,以MN为直径的半圆与线段AB相切于点P.
设点M的坐标为(m,n).
①当点M在第一或第三象限时,m=2n.
把点M的坐标(2n,n)代入抛物线的解析式得n2-n-1=0,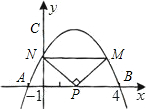
解之得n=
.
∴点M的坐标是(1+
,
)或(1-
,
).
②当点M在第二或第四象限时,m=-2n.
把点M的坐标(-2n,n)代入抛物线的解析式得n2+2n-1=0,
解之得n=-1±
.
∴点M的坐标是(2-2
,-1+
)或(2+2
,-1-
).
综上,满足条件的点M的坐标是(1+
,
),(1-
,
),
(2-2
,-1+
),(2+2
,-1-
).
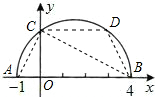
如图,连接AC,CB.依相交弦定理的推论可得OC2=OA•OB,
解得OC=2.
故C点的坐标为(0,2).
(2)设抛物线解析式为y=a(x+1)(x-4).
把点C(0,2)的坐标代入上式得a=-
| 1 |
| 2 |
∴抛物线解析式是y=-
| 1 |
| 2 |
| 3 |
| 2 |
(3)如图,过点C作CD∥OB,交抛物线于点D,则四边形BOCD为直角梯形.
由(2)知抛物线的对称轴是x=
| 3 |
| 2 |
∴点D的坐标为(3,2).
设过点B,点D的解析式是y=kx+b.
把点B(4,0),点D(3,2)的坐标代入上式得
|
解之得
|
∴直线BD的解析式是y=-2x+8.
(4)依题意可知,以MN为直径的半圆与线段AB相切于点P.
设点M的坐标为(m,n).
①当点M在第一或第三象限时,m=2n.
把点M的坐标(2n,n)代入抛物线的解析式得n2-n-1=0,

解之得n=
1±
| ||
| 2 |
∴点M的坐标是(1+
| 5 |
1+
| ||
| 2 |
| 5 |
1-
| ||
| 2 |
②当点M在第二或第四象限时,m=-2n.
把点M的坐标(-2n,n)代入抛物线的解析式得n2+2n-1=0,
解之得n=-1±
| 2 |
∴点M的坐标是(2-2
| 2 |
| 2 |
| 2 |
| 2 |
综上,满足条件的点M的坐标是(1+
| 5 |
1+
| ||
| 2 |
| 5 |
1-
| ||
| 2 |
(2-2
| 2 |
| 2 |
| 2 |
| 2 |


练习册系列答案
相关题目
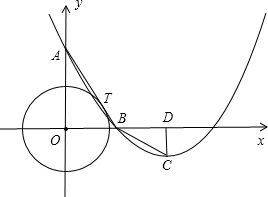 A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-
A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-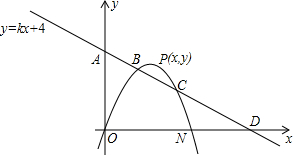 A的面积等于△PON面积的
A的面积等于△PON面积的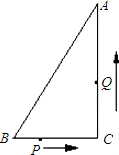 别从B、C同时运动,请解答下面的问题,并写出探索的主要过程:
别从B、C同时运动,请解答下面的问题,并写出探索的主要过程: