题目内容
【题目】平面直角坐标系xOy中,对于点P(x,y)和Q(﹣x,y′),给出如下定义: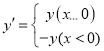 ,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
根据定义,解答下列问题;
(1)点(3,4)的“可控变点”为点 .
(2)点P1的“可控变点”为点P2,点P2的“可控变点”为点P3,点P3的“可控变点”为点P4,…,以此类推.若点P2018的坐标为(3,a),则点P1的坐标为 .
(3)若点N(a,3)是函数y=﹣x+4图象上点M的“可控变点”,求点M的坐标.
【答案】(1)(-3,4),(2)(-3,a),(3)(1,3).
【解析】
(1)依据“可控变点”的定义可得,点(3,4)的“可控变点”为点(﹣3,4);
(2)依据变化规律可得每四次变化出现一次循环,即可得到当点P2018的坐标为(3,a),则点P1的坐标为(﹣3,﹣a);
(3)分两种情况讨论:当﹣a≥0时,a≤0;当﹣a<0时,a>0,分别把点M的坐标代入函数y=﹣x+4即可得到结论.
解:(1)∵x=3>0,
∴根据“可控变点”的定义可得,点(3,4)的“可控变点”为点(﹣3,4),
故答案为:(﹣3,4);
(2)当x≥0时,点P1(x,y)的“可控变点”为点P2(﹣x,y),点P2(﹣x,y)的“可控变点”为点P3(x,﹣y),点P3(x,﹣y)的“可控变点”为点P4(﹣x,﹣y),点P4(﹣x,﹣y)的“可控变点”为点P5(x,y),…,故每四次变化出现一次循环;
当x<0时,同理可得每四次变化出现一次循环;
∵2018=4×504+2,
∴当点P2018的坐标为(3,a),则点P1的坐标为(﹣3,﹣a),
故答案为:(﹣3,﹣a);
(3)由题意知,点M的横坐标为﹣a.
当﹣a≥0时,a≤0,此时点M(﹣a,3).
代入y=﹣x+4,得3=a+4,a=﹣1,符合题意,
∴点M的坐标为(1,3);
当﹣a<0时,a>0,此时点M(﹣a,﹣3).
代入y=﹣x+4,得﹣3=a+4,a=﹣7,不合题意,舍去.
综上所述,点M的坐标为(1,3).

【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.