题目内容
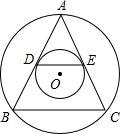如图，两个同心圆，大圆的弦AB和AC分别切小圆于点D，E．求证：DE∥BC．
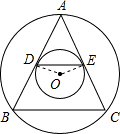证明：连接OD、OE，则OD⊥AB，OE⊥AC，
由垂径定理得：AD=BD，AE=CE，
∴DE∥BC．
分析：连接OD，OE，根据切线性质求出OD⊥AB，OE⊥AC，根据垂径定理求出AD=BD，AE=CE，根据三角形的中位线定理求出即可．
点评：本题考查了三角形的中位线定理，垂径定理，切线的性质等知识点的应用，主要培养学生运用定理进行推理的能力，题型较好．
练习册系列答案
相关题目
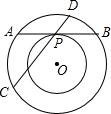如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD=13，PD=4，则两圆组成的圆环的面积是（ ）| A、16π | B、36π | C、52π | D、81π |
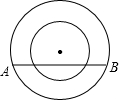如图，两个同心圆，大圆半径为5cm，小圆的半径为4cm，若大圆的弦AB与小圆有两个公共点，则AB的取值范围是
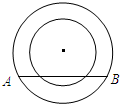（2012•兰州）如图，两个同心圆，大圆半径为5cm，小圆的半径为3cm，若大圆的弦AB与小圆相交，则弦AB的取值范围是
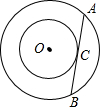如图，两个同心圆，大圆的弦AB与小圆相切于点C，若AB=10，则两个同心圆之间的圆环面积是
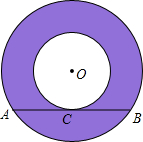如图是两个同心圆，大圆的弦AB与小圆相切于点C，AB=6cm，则图中圆环面积为