Question

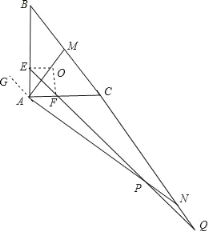
【题目】已知在△ABC中，∠BAC＝90°，M是边BC的中点，BC的延长线上的点N满足AM⊥AN．△ABC的内切圆与边AB、AC的切点分别为E、F，延长EF分别与AN、BC的延长线交于P、Q，则＝（　　）

A. 1B. 0.5C. 2D. 1.5

Answer 1

【答案】A

【解析】

取△ACB的内切圆的圆心是O，连接OE、OF，得出正方形AEOF，求出AE＝AF，推出∠AEF＝∠AFE＝∠CFQ，根据直角三角形斜边上中线性质求出AM＝MC，推出∠MCA＝∠MAC，根据∠BAC＝∠MAG＝∠MAN＝90°，求出∠GAE＝∠MAC＝∠MCA，∠EAM＝∠CAP，根据三角形的外角性质得出∠GAE＝∠APE+∠AEP，∠MCA＝∠Q+∠CFQ，求出∠Q＝∠NPQ，推出PN＝NQ即可．

取△ACB的内切圆的圆心是O，连接OE、OF，作NA的延长线AG，

则OE⊥AB，OF⊥AC，OE＝OF，

∵∠BAC＝90°，

∴四边形AEOF是正方形，

∴AE＝AF，

∴∠AEF＝∠AFE，

∵∠BAC＝90°，M为斜边BC上中线，

∴AM＝CM＝BM，

∴∠MAC＝∠MCA，

∵∠BAC＝90°，AN⊥AM，

∴∠BAC＝∠MAG＝∠MAN＝90°，

∴∠GAE+∠EAM＝90°，∠EAM+∠MAC＝90°，∠MAC+∠CAN＝90°，

∴∠GAE＝∠MAC＝∠MCA，∠EAM＝∠CAP，

∵∠GAE＝∠APE+∠AEP，∠MCA＝∠Q+∠CFQ，

∵∠AEF＝∠AFE＝∠CFQ，∠EPA＝∠NPQ，

∴∠Q＝∠NPQ，

∴PN＝QN，

∴＝1，

故选：A．