题目内容
阅读下面的材料:
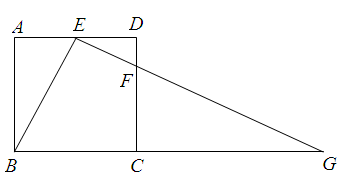
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果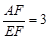 ,求
,求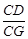 的值.
的值.
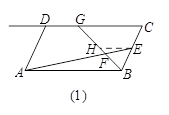
他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 ,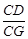 的值为 .
的值为 .
(2)如图(2),在原题的其他条件不变的情况下,如果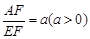 ,那么
,那么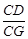 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).
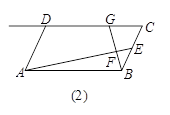
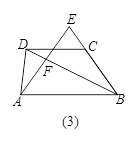
(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果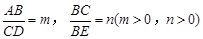 ,那么
,那么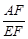 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果
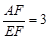 ,求
,求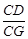 的值.
的值. 
他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 ,
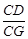 的值为 .
的值为 .(2)如图(2),在原题的其他条件不变的情况下,如果
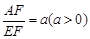 ,那么
,那么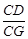 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).
(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果
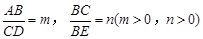 ,那么
,那么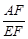 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
(1)3,2,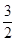 ;(2)
;(2)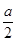 ;(3)mn.
;(3)mn.
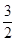 ;(2)
;(2)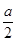 ;(3)mn.
;(3)mn.试题分析:(1)过E点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH来表示,最后求得比值;
(2)先作EH∥AB交BG于点H,得出△EFH∽△AFB,即可得出
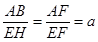 ,再根据AB=CD,表示出CD,根据平行线的性质得出△BEH∽△BCG,即可表示出
,再根据AB=CD,表示出CD,根据平行线的性质得出△BEH∽△BCG,即可表示出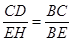 ,从而得出
,从而得出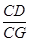 的值;
的值;(3)先过点E作EH∥AB交BD的延长线于点H,得出EH∥AB∥CD,根据EH∥CD,得出△BCD∽△BEH,再进一步证出△ABF∽△EHF,从而得出
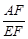 的值.
的值.试题解析:(1)过点E作EH∥AB交BG于点H,
则有△ABF∽△HEF,
∴
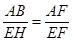 ,
,∴AB=3EH.
∵平行四边形ABCD中,EH∥AB,
∴EH∥CD,
又∵E为BC中点,
∴EH为△BCG的中位线,
∴CG=2EH,
∴
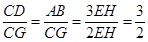 ;
;(2)作EH∥AB交BG于点H,则△EFH∽△AFB,
∴
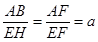 ,
,∴AB=aEH.
∵AB=CD,
∴CD=aEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴
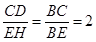 ,
,∴CG=2EH.
∴
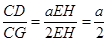 ;
;(3)过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD,
∵EH∥CD,
∴△BCD∽△BEH,
∴
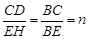 ,
,∴CD=nEH.
又
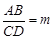 ,
,∴AB=mCD=mnEH.
∵EH∥AB,
∴△ABF∽△EHF,
∴
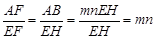 .
.
练习册系列答案
相关题目
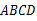 中,
中,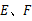 分别是边
分别是边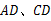 上的点,
上的点,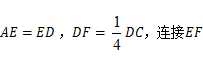 并延长交
并延长交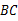 的延长线于点
的延长线于点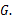
 ;
; 的长.
的长.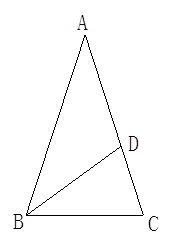
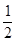 ,则点的对应点′的坐标是
,则点的对应点′的坐标是 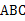 如图所示,则下列4个三角形中,与△
如图所示,则下列4个三角形中,与△