题目内容
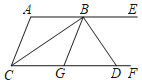
【题目】如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)

(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
【答案】(1)见解析;(2)见解析;(3)∠CAD=∠BDP+∠DPB.
【解析】
(1)根据三角形的内角和即可得到结论;
(2)根据三角形的内角和得到∠B=∠CDE,得到MN∥BA,根据平行线的性质证明;
(3)根据三角形的外角性质证明.
(1)∵∠C+∠CAD+∠ADC=∠C+∠CAB+∠B=180°,
∴∠CAD+∠ADC=∠CAB+∠B,
∵∠CDA=∠CAB,
∴∠CAD=∠B,
∵∠CAB=∠CAD+∠DAB=∠ABC+∠DAB,
∴∠CDA=∠DAB+∠DBA;
(2)∵∠CDA=∠CAB,∠C=∠C,
∴180°-∠CDA-∠C=180°-∠CAB -∠C
∴∠B=∠CAD,
∵∠CDE=∠CAD,
∴∠B=∠CDE,
∴MN∥BA,
∴∠AED+∠EAB=180°;
(3)∠CAD=∠BDP+∠DPB
证明:由三角形的外角的性质可知,∠ABC=∠BDP+∠DPB,
∵∠CDA=∠CAB,∠C=∠C,
∴∠B=∠CAD,
∴∠ABC=∠BDP+∠DPB.
∴∠CAD=∠BDP+∠DPB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目