题目内容
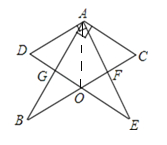
【题目】如图,两块完全相同的含30°的直角三角板叠放在一起,且∠DAB=30°,有以下四个结论,①AF⊥BC;②∠BOE=135°;③O为BC中点;④AG:DE=1:3,其中正确结论的序号是( )
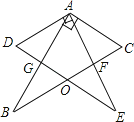
A.①②B.②④C.②③D.①③
【答案】D
【解析】
①根据已知得出∠CAF=30°,∠GAF=60°,进而得出∠AFB的度数;
②在四边形ADOC中,根据四边形的内角和为360°可得出∠DOC的度数,继而得出∠BOE的度数;
③利用△AGO≌△AFO,得出AO=CO=AC,进而得出BO=CO=AO,即O为BC的中点;
④利用假设DG=x,∠DAG=30°,得出AG=![]() x,GE=3x,DE=4x,进而得出答案.
x,GE=3x,DE=4x,进而得出答案.
解:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.
∴∠GAF=60°,∠CAF=30°,∠C=∠D=60°,
∴∠AFB=∠C+∠CAF=90°,
①AF⊥BC正确;
由①可得∠C=∠D=60°,∠DAC=120°,
∵∠C+∠D+∠DAC+∠DOC=360°,
∴∠DOC=120°,
∵∠DOC=∠BOE,
∴∠BOE=120°,
即②∠BOE=135°错误;
连接AO,
∵两块完全相同的含30°的直角三角板叠放在一起,且∠DAB=30°,
∴AD=AC,∠DAG=∠CAF,∠D=∠C=60°,
∴△ADG≌△ACF(AAS),
∴AG=AF,
∵AO=AO,∠AGO=∠AFO=90°,
∴△AGO≌△AFO(SAS),
∴∠OAF=∠OAG=30°,
∴∠OAC=60°,
∵∠C=60°,
∴AO=CO=AC,
∵∠OAG=∠B=30°,
∴BO=AO,
∴BO=CO,
即可得③O为BC中点正确;
假设DG=x,
∵∠DAG=30°,
∴AG=![]() x,AD=2x,DE=4x,
x,AD=2x,DE=4x,
∴GE=3x,
故可得AG:DE=![]() :4,即④错误;
:4,即④错误;
综上可得①③正确.
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案