��Ŀ����
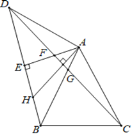
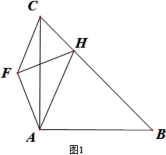
����Ŀ�� (1)��ͼ1������Rt��ABC�У���CAB=90������H��BC���ϣ���AH��������Rt��HFA����HFA=90����֤��AF=CF.
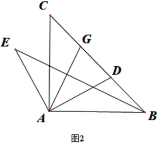
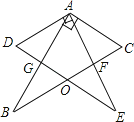
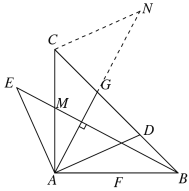
(2)��ͼ2������Rt��ABC�У���CAB=90����D��BC�ϣ�AD��AE,AD=AE,GΪCD�е㣬��֤��AG��BE
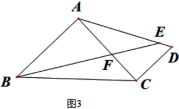
(3)��ͼ3������Rt��ABC�У���BAC=90������C��CD��AB, CD=8����AD,��AD��ȡһ��EʹAE=AB����BE��AC��F����AF=9����AD= .
���𰸡���1������������2������������3��17.
��������
��1����AHΪֱ����ԲO����BC���ڵ�E���ɵá�AEC=90�㣬�ɵ������������ߺ�һ��֪AEΪBC���ϵ����ߣ�����EA=EC������Բ�ܽǶ����Ƴ���AEF=��AHF=45��=��CEF���ٴ��ɵ������������ߺ�һ��֪EF��ֱƽ��AC�����ɵ�֤��
��2���ӳ�AG��N��ʹGN=AG������CN����֤��AGD�ա�NGC��Ȼ���Ƴ���ACN=��BAE����֤����ACN�ա�BAE���õ���CAN=��ABE�����ɵó����ۣ�
��3���ӳ�BE��CD����G����DG=DE����CF=a����AC=AB=AE=AF+CF=9+a�������������ζ�Ӧ�߳ɱ�������a��ʾ��CG��DE��AD��Ȼ���ù��ɶ��������������.
֤������1����ͼ��ʾ����AHΪֱ����ԲO����BC���ڵ�E��

���AEC=90�㣬��AE��BC��
��AB=AC
��AEΪBC���ϵ����ߣ�
��EA=EC
�ɡߡ�AEF=��AHF=45��
���CEF=90��-45��=45��
���AEF=��CEF
�ɵ������������ߺ�һ�ɵ�EF��ֱƽ��AC��
��AF=CF
��2���ӳ�AG��N��ʹGN=AG������CN��
��GΪCD�е㣬
��CG=DG��
�ڡ�AGD�͡�NGC�У�
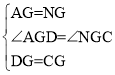
���AGD�ա�NGC��SAS��
���DAG=��N��AD=NC����ADG=��NCG
��AE=AD
��AE=NC
�ߡ�EAC+��CAD=90�㣬��BAD+��CAD=90�㣬
���EAC=��BAD
�ߡ�ADG=��BAD+��ABD=��BAD+45��
���ACN=��NCG+45��=��BAD+90��
�֡ߡ�BAE=��EAC+90��
���ACN=��BAE
�ڡ�ACN�͡�BAE�У�
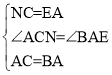
���ACN�ա�BAE��SAS��
���CAN=��ABE
�֡ߡ�ABE+��AMB=90��
���CAN+��AMB=90��
��AG��BE
��3����ͼ���ӳ�BE��CD����G��

��AB��CD
���ACD=��BAC=90�㣬��G=��ABE
�֡�AB=AE��
���ABE=��AEB��
��AEB=��DEG
���G=��DEG
��DG=DE
��CF=a����AC=AB=AE=AF+CF=9+a
��AB��CD��
���ABF�ס�CGF
��![]() ����
����![]()
���![]()
��DE=DG=CG-CD=![]()
��AD=AE+DE=![]()
��Rt��ACD��AC2+CD2=AD2
��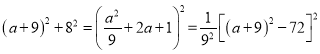
��![]() ����ԭ���̱���Ϊ
����ԭ���̱���Ϊ![]()
������![]() �����x=0��225
�����x=0��225
��![]() ��
��![]()
��ȥ������![]()
��AD=![]()
�ʴ�Ϊ��17.