题目内容
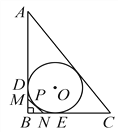
【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E，过劣弧
(不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若AC=10，BC=6，则△MBN的周长为__.
【答案】4
【解析】根据勾股定理，由Rt△ABC中AC=10，BC=6，求得AB=8，
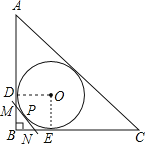
如图，连接OD、OE，由切线的性质，⊙O是Rt△ABC的内切圆，得到OD⊥AB，OE⊥BC，根据有三个角是直角的四边形为矩形得四边形ODBE是矩形，然后由OD=OE，得到矩形ODBE是正方形，根据面积相等的关系，求得BD=BE=OD=OE=2，最后根据切线长定理，由⊙O切AB于D，切BC于E，切MN于P，知MP=DM，NP=NE，从而求得Rt△MBN的周长为：MB+NB+MN=MB+BN+NE+DM=BD+BE=2+2=2r.
故选：C．
练习册系列答案
相关题目
