题目内容
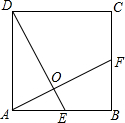正方形ABCD中，E、F分别为AB、BC的中点，AF与DE相交于点O，则| AO | DO |
分析：本题可通过相似三角形求解，根据所求的条件可判断出需证明△OAE∽△ADE，已知了公共角∠OEA，缺少∠OAE=∠ADE的条件；因此可通过证△ADE和△BAF全等来得出∠OAE=∠ADE，由此可得解．
解答：解：∵AD=AB，AE=BF，∠DAE=∠B=90°；
∴△ADE≌△BAF（SAS）；
∴∠ADE=∠OAE；
又∵∠OEA=∠AED，
∴△OAE∽△ADE；
∴
=
=
．
∴△ADE≌△BAF（SAS）；
∴∠ADE=∠OAE；
又∵∠OEA=∠AED，
∴△OAE∽△ADE；
∴
| AO |
| DO |
| AE |
| AD |
| 1 |
| 2 |
点评：此题综合考查三角形全等的判定和相似三角形的判定．
练习册系列答案
相关题目
（2013•临沂）如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
如图，在正方形ABCD中，画2个半径为a的四分之一圆，用代数式表示阴影部分的面积为
如图，在正方形ABCD中，AB=4，E在BC边上，BE=1，F是AC上一动点，则EF+BF的最小值是