题目内容
在边长为1的正方形ABCD中,点M、N、O、P分别在边AB、BC、CD、DA上.如果AM=BM,DP=3AP,则MN+NO+OP的最小值是分析:作点M关于直线BC的对称点M′,过P作关于直线CD的对称点P′,根据两点间线段最短,及勾股定理即可求解.
解答: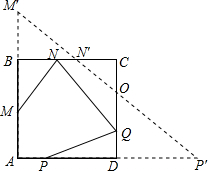 解:作点M关于直线BC的对称点M′,过P作关于直线CD的对称点P′,连M′P′交BC,CD于N,O,
解:作点M关于直线BC的对称点M′,过P作关于直线CD的对称点P′,连M′P′交BC,CD于N,O,
所以M′N=MN,OP=OP′
MN+NO+OP=NM′+ON+OP′=M′P′
此时MN+NO+OP有最小值,
由作法,得BM′=BM=
,所以AM′=3/2,
DP′=3/4,AP′=1+3/4=7/4
在直角三角形AM′P′中,M′P′2=AM′2+AP′2=
,
所以M′P′=
.
故答案为:
.
 解:作点M关于直线BC的对称点M′,过P作关于直线CD的对称点P′,连M′P′交BC,CD于N,O,
解:作点M关于直线BC的对称点M′,过P作关于直线CD的对称点P′,连M′P′交BC,CD于N,O,所以M′N=MN,OP=OP′
MN+NO+OP=NM′+ON+OP′=M′P′
此时MN+NO+OP有最小值,
由作法,得BM′=BM=
| 1 |
| 2 |
DP′=3/4,AP′=1+3/4=7/4
在直角三角形AM′P′中,M′P′2=AM′2+AP′2=
| 85 |
| 16 |
所以M′P′=
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:考查了正方形的性质和轴对称-最短路线问题,熟知正方形的性质是解答此题的关键.

练习册系列答案
相关题目
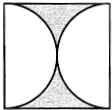 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?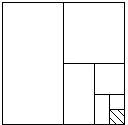 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.