题目内容
【题目】如图,在等边三角形ABC右侧作射线CP,∠ACP=![]() (0°<
(0°<![]() <60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.
<60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.

(1)求∠DBC的大小(用含![]() 的代数式表示);
的代数式表示);
(2)在![]() (0°<
(0°<![]() <60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.
【答案】(1)∠DBC![]() ;(2)∠AEB的大小不会发生变化,且∠AEB=60°;(3)BD=2AE+CE,证明见解析.
;(2)∠AEB的大小不会发生变化,且∠AEB=60°;(3)BD=2AE+CE,证明见解析.
【解析】
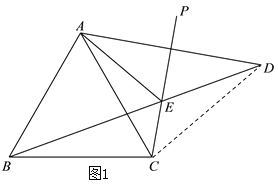
(1)如图1,连接CD,由轴对称的性质可得AC=DC,∠DCP=∠ACP=![]() ,由△ABC是等边三角形可得AC=BC,∠ACB=60°,进一步即得∠BCD=
,由△ABC是等边三角形可得AC=BC,∠ACB=60°,进一步即得∠BCD=![]() ,BC=DC,然后利用三角形的内角和定理即可求出结果;
,BC=DC,然后利用三角形的内角和定理即可求出结果;
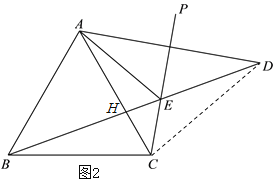
(2)设AC、BD相交于点H,如图2,由轴对称的性质可证明△ACE≌△DCE,可得∠CAE=∠CDE,进而得∠DBC=∠CAE,然后根据三角形的内角和可得∠AEB=∠BCA,即可作出判断;
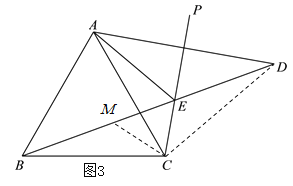
(3)如图3,在BD上取一点M,使得CM=CE,先利用三角形的外角性质得出∠BEC![]() ,进而得△CME是等边三角形,可得∠MCE=60°,ME=CE,然后利用角的和差关系可得∠BCM=∠DCE,再根据SAS证明△BCM≌△DCE,于是BM=DE,进一步即可得出线段AE,BD,CE之间的数量关系.
,进而得△CME是等边三角形,可得∠MCE=60°,ME=CE,然后利用角的和差关系可得∠BCM=∠DCE,再根据SAS证明△BCM≌△DCE,于是BM=DE,进一步即可得出线段AE,BD,CE之间的数量关系.
解:(1)如图1,连接CD,∵点A关于射线CP的对称点为点D,∴AC=DC,∠DCP=∠ACP=![]() ,
,
∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,
∴∠BCD=![]() ,BC=DC,
,BC=DC,
∴∠DBC=∠BDC![]() ;
;
(2)∠AEB的大小不会发生变化,且∠AEB=60°.
理由:设AC、BD相交于点H,如图2,∵点A关于射线CP的对称点为点D,
∴AC=DC,AE=DE,又∵CE=CE,∴△ACE≌△DCE(SSS),∴∠CAE=∠CDE,
∵∠DBC=∠BDC,∴∠DBC=∠CAE,又∵∠BHC=∠AHE,∴∠AEB=∠BCA=60°,
即∠AEB的大小不会发生变化,且∠AEB=60°;
(3)AE,BD,CE之间的数量关系是:BD=2AE+CE.
证明:如图3,在BD上取一点M,使得CM=CE,
∵∠BEC=∠BDC+∠DCE=![]() ,
,
∴△CME是等边三角形,∴∠MCE=60°,ME=CE,
∴![]() ,
,
∴∠BCM=∠DCE,又∵BC=DC,CM=CE,
∴△BCM≌△DCE(SAS),∴BM=DE,
∵AE=DE,
∴BD=BM+ME+DE=2DE+ME=2AE+CE.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案






