题目内容
如图，已知矩形ABCD的边AD长为4cm，边AB长为3cm，从中截去一个矩形（图中阴影部分），如果所截矩形与原矩形相似，那么所截矩形的面积是（ ）分析：根据题意，截取矩形与原矩形相似，利用相似形的对应边的比相等可得．
解答：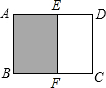
解：依题意，在矩形ABDC中截取矩形ABFE，
则矩形ABDC∽矩形AEFB，
则
=
，
设AE=xcm，得到：
=
，
解得：x=2.25，
则截取的矩形面积是：3×2.25=6.75cm2．
故选D．
解：依题意，在矩形ABDC中截取矩形ABFE，则矩形ABDC∽矩形AEFB，
则
| AB |
| AE |
| AD |
| AB |
设AE=xcm，得到：
| 3 |
| x |
| 4 |
| 3 |
解得：x=2.25，
则截取的矩形面积是：3×2.25=6.75cm2．
故选D．
点评：本题就是考查相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
练习册系列答案
相关题目
如图，已知矩形DEFG内接于Rt△ABC，D在AB上，E、F在BC上，G在AC上，∠BAC=90°，AB=6cm，AC=8cm，
m/秒的速度移动，如果M、N两点同时出发，移动的时间为x秒（0≤x≤6）．
点A运动．
（2012•宁德质检）如图，已知Rt△ABC，∠B=90°，AB=8，BC=6，把斜边AC平均分成n段，以每段为对角线作边与AB、BC平行的小矩形，则这些小矩形的面积和是（ ）
如图，已知矩形ABCD中AB：BC=3：1，点A、B在x轴上，直线y=mx+n（0＜m＜n＜