题目内容
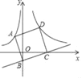
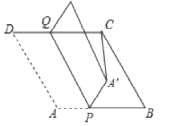
【题目】如图,在菱形ABCD中,AB=8,∠B=60°,P是AB上一点,BP=5,Q是CD边上ー动点,将四边形APQD沿直线PQ折叠,A的对应点A`.当CA`的长度最小时,则CQ的长为( )
A. 7B. 2![]() C. 2
C. 2![]() D. 4
D. 4![]()
【答案】A
【解析】
由A`P=3可知点A`在以P为圆心以PA`为半径的弧上,故此当C,P,A`在一条直线上时,CA`有最小值,过点C作CH⊥AB,垂足为H,先求得BH、HC的长,则可得到PH的长,然后再求得PC的长,最后依据折叠的性质和平行线的性质可证明△CQP为等腰三角形,则可得到Q℃的长
如图所示:过点C作CH⊥AB,垂足为H
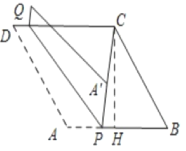
在Rt△BCH中,∠B=60°,BC=8,则
BH=![]() BC=4,CH=sin60°BC=
BC=4,CH=sin60°BC=![]()
![]() 8=4
8=4![]() .
.
∴PH=1
在Rt△CPH中,依据勾股定理可知
PC=![]()
由翻折的性质可知:∠APQ=∠A'PQ
∵DC∥AB
∴∠CQP=∠APQ
∴∠CQP=∠CPQ.
∴QC=CP=7.
故选:A

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
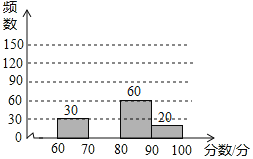
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?