题目内容
5.若一直角三角形的两边长分别为12和5,那么斜边上的中线长为6.5或6.分析 分为两种情况①当AC=5,BC=12时,由勾股定理求出AB,根据直角三角形斜边上中线得出CD=$\frac{1}{2}$AB,求出即可;②当AC=5,AB=12时,根据直角三角形斜边上中线得出CD=$\frac{1}{2}$AB,求出即可.
解答 解: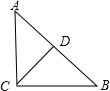
分为两种情况:①当AC=5,BC=12时,由勾股定理得:AB=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵CD是斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=6.5;
②当AC=5,AB=12时,
∵CD是斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=6;
即CD=6.5或6,
故答案为:6.5或6.
点评 本题考查了勾股定理和直角三角形斜边上中线性质,注意:注意:①直角三角形斜边上中线等于斜边的一半,②要进行分类讨论.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
16. 如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
 如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )| A. | 15 | B. | 16 | C. | 19 | D. | 20 |
13.在平面直角坐标系中,点A(2016,2017)关于原点O对称的点A′的坐标为( )
| A. | (-2016,2017) | B. | (2016,-2017) | C. | (2016,2017) | D. | (-2016,-2017) |
15.下列命题不一定成立的是( )
| A. | 斜边与一条直角边对应成比例的两个直角三角形相似 | |
| B. | 两个等腰直角三角形相似 | |
| C. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| D. | 各有一个角等于100°的两个等腰三角形相似 |
 一跨河桥,桥拱是圆弧形,跨度(AB)为12米,拱高(CN)为2米,
一跨河桥,桥拱是圆弧形,跨度(AB)为12米,拱高(CN)为2米,