Question

定义{a，b，c}为函数y=ax²+bx+c的“特征数”．如：函数y=x²-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3}，函数y=-x的“特征数”是{0，-1，0}
（1）将“特征数”是{0，

3

3

，1}的函数图象向下平移2个单位，得到一个新函数，这个新函数的解析式是y=

3

3

x-1；
（2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=

3

分别交于D、C两点，判断以A、B、C、D四点为顶点的四边形形状，请说明理由并计算其周长；
（3）若（2）中的四边形与“特征数”是{1，-2b，b2+

1

2

}的函数图象的有交点，求满足条件的实数b的取值范围．

Answer 1

分析：（1）根据函数“特征数”写出函数的解析式，再根据平移后一次函数的变化情况写出函数图象向下平移2个单位的新函数的解析式．
（2）判断以A、B、C、D四点为顶点的四边形形状，可根据一次函数图象向下平移2个单位与原函数图象的关系，得出AB=2，并确定为平行四边形，由直线相交计算交点坐标后，求出线段BC=2，再根据菱形的判定（邻边相等的平行四边形是菱形）得出，其周长=2×4=8；
（3）根据函数“特征数”写出二次函数的解析式，化为顶点式为y=（x-b）²+

1

2

，确定二次函数的图象不会经过点B和点C，再将菱形顶点A（0，1），D（

3

，2）代入二次函数解析式得出实数b的取值范围．

解答：解：（1）y=

3

3

x-1（1分）“特征数”是{0，

3

3

，1}的函数，
即y=

3

3

+1，
该函数图象向下平移2个单位，得y=

3

3

x-1．

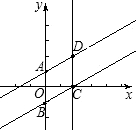
（2）由题意可知y=

3

3

x+1向下平移两个单位得y=

3

3

x-1
∴AD∥BC，AB=2．
∵x=

3

，
∴AB∥CD．
∴四边形ABCD为平行四边形．

x= 3 y= 3 3 x-1

，
得C点坐标为（

3

，0），
∴D（

3

，2）
由勾股定理可得BC=2
∵四边形ABCD为平行四边形，AB=2，BC=2
∴四边形ABCD为菱形．
∴周长为8．

（3）二次函数为：y=x²-2bx+b²+

1

2

，化为顶点式为：y=（x-b）²+

1

2

，
∴二次函数的图象不会经过点B和点C．
设二次函数的图象与四边形有公共部分，
当二次函数的图象经过点A时，将A（0，1），代入二次函数，
解得b=-

2

2

，b=

2

2

（不合题意，舍去），
当二次函数的图象经过点D时，
将D（

3

，2），代入二次函数，
解得b=

3

+

6

2

，b=

3

-

6

2

（不合题意，舍去），
所以实数b的取值范围：-

2

2

≤b≤

3

+

6

2

．

点评：本题结合“特征数”的定义考查一次函数，二次函数的综合应用，综合性强，能力要求高．