题目内容
解方程(组):(1)解分式方程:
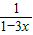 -
- =
=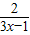
(2)解方程组:
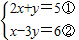
【答案】分析:(1)观察方程知,最简公分母为2(1-3x),方程两边乘以2(1-3x),化为整式方程求解;
(2)由于未知数的系数为1时,可选用代入法求解.
解答:解:(1) -
- =-
=-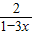 ,
,
两边同乘以2(1-3x),
得:2-3(1-3x)=-4,
整理,得:9x=-3
解得:x=- ,
,
经检验,x=- 是原方程的根;
是原方程的根;
(2)①-②×2,得:7y=-7
解得:y=-1.
把y=-1代入①解得x=3,
故方程的解为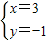 .
.
点评:(1)解分式方程主要是将分式方程转化为整式方程求解,求解后进行检验;
(2)当未知数的系数为1时,可选用代入法求解;当未知数的系数互为相反数时,可选用加减消元法进行求解.方程组较复杂时,需先化简.
(2)由于未知数的系数为1时,可选用代入法求解.
解答:解:(1)
 -
- =-
=-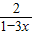 ,
,两边同乘以2(1-3x),
得:2-3(1-3x)=-4,
整理,得:9x=-3
解得:x=-
 ,
,经检验,x=-
 是原方程的根;
是原方程的根;(2)①-②×2,得:7y=-7
解得:y=-1.
把y=-1代入①解得x=3,
故方程的解为
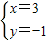 .
.点评:(1)解分式方程主要是将分式方程转化为整式方程求解,求解后进行检验;
(2)当未知数的系数为1时,可选用代入法求解;当未知数的系数互为相反数时,可选用加减消元法进行求解.方程组较复杂时,需先化简.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目