题目内容
在直角坐标系xOy中,已知抛物线y=ax2+bx+c的开口向上,顶点P在直线y=-4x上,且P到坐标原点距离为 ,又知抛物线与x轴两交点A、B(A在B的左侧)的横坐标的平方和为10.
,又知抛物线与x轴两交点A、B(A在B的左侧)的横坐标的平方和为10.
(1)求此抛物线的解析式.
(2)若Q是抛物线上异于A、B、P的点,且∠QAP=90°,求点Q的坐标.(利用“点坐标的绝对值等于线段长”沟通函数与几何,转化为点坐标用函数知识,转化为线段长用几何知识)
解: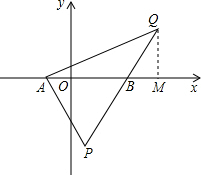
(1)∵顶点P在直线y=-4x上,
可设P(a1,-4a),则有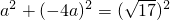 ,
,
解得:a=±1,
∴P(1,-4)或(-1,4).
∵抛物线开口向上,又与x轴有交点,
∴(-1,4)不合题意舍去.
设y=a(x-1)2-4=ax2-2ax+a-4与x轴交于点A(x1,0)、
B({x2,0),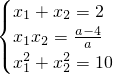 ,
,
消x1、x2,
解得a=1;
(2)如图所示,设抛物线上点Q(m,n),过Q作QM⊥x轴于点M. ,
,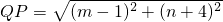 ,
,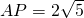 ,
,
∵∠QAP=90°,由勾股定理,得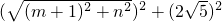 =(m-1)2+(n+4)2,
=(m-1)2+(n+4)2,
整理,得m-2n+1=0,又n=m2-2m-3.
解得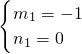 (不合题意舍去)或
(不合题意舍去)或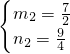 .
.
∴Q(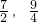 ).
).
分析:(1)由顶点P在直线y=-4x上,且P到坐标原点距离为
 ,可得出点P的坐标,再利用勾股定理可以解决,
,可得出点P的坐标,再利用勾股定理可以解决,(2)假设出点Q的坐标,表示出AQ,QP的长度,利用勾股定理可以解决.
点评:此题主要考查了二次函数与一次函数综合应用,以及勾股定理的应用,计算量较大,应认真计算.

练习册系列答案
相关题目

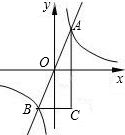 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.