题目内容
【题目】如图△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BD=5,CE=8,则DE的长为 .
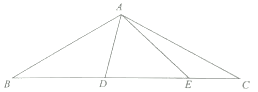
【答案】7.
【解析】
试题解析:∵AB=AC,
∴可把△AEC绕点A顺时针旋转120°得到△AE′B,如图,
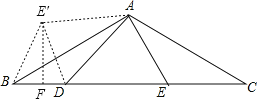
∴BE′=EC=8,AE′=AE,∠E′AB=∠EAC,
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠EAC=60°,
∴∠E′AD=∠E′AB+∠BAD=60°,
在△E′AD和△EAD中
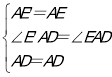
∴△E′AD≌△EAD(SAS),
∴E′D=ED,
过E′作EF⊥BD于点F,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠C=∠E′BA=30°,
∴∠E′BF=60°,
∴∠BE′F=30°,
∴BF=![]() BE′=4,E′F=4
BE′=4,E′F=4![]() ,
,
∵BD=5,
∴FD=BD-BF=1,
在Rt△E′FD中,由勾股定理可得E′D=![]() ,
,
∴DE=7.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目