题目内容
【题目】如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,单位秒).
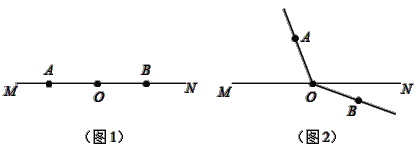
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
【答案】(1)60°;(2)t=![]() ;(3)t=
;(3)t=![]() 或
或![]() .
.
【解析】
(1)当t=10时,∠AOM=18°×10=180°,即OA与ON重合,故
∠AOB=∠BON=60°.
(2)求OA追上OB的大致时刻,得到OM平分∠AOB时的图形,用t表示此时
∠AOM与∠BOM的度数,列方程即可求t.
(3)OA、OB都是顺时针旋转,可理解为初始路程差为180°的追及问题:
当∠AOB第一次达到45°时,OA差300追上OB,路程差为(180-45)°即得18t-6t=180-45;当∠AOB第二次达到45°时,OA追上OB且超过45°,路程差为(180+45)°;
当∠AOB第三次达到45°时,OA再走一圈差45°追上OB,路程差为多转了(180+360-45)°,此时求出的t大于30故不需再求.
(1)当t=10时,∠AOM=18°×10=180°,∠BON=6°×10=60°
∠AOB=180°-∠AOM+∠BON=60°故答为60°.
(2)存在满足条件的t值.
OA旋转一周所需时间为:360°÷18=20秒,
此时∠BON=6°×20=120°,即OA已经旋转过OB的位置,
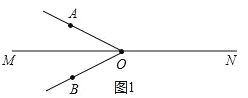
若OM平分∠AOB且0°<∠AOB<180°位置如图1,
∴∠AOM=(18t-360)°,∠BOM=(180-6t)°
∴18t-360=180-6t,解得t=![]() ,
,
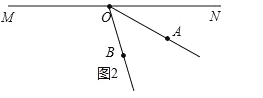
(3)如图2,当∠AOB第一次达到45°时,OA比OB多转了(180-45)°
得18t-6t=180-45,解得t=![]() ,
,
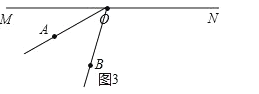
如图3,当∠AOB第二次达到45°时,OA比OB多转了(180+45)°,
得18t-6t=180+45,解得t=![]() ,
,
当∠AOB第三次达到45°时,OA比OB多转了(180+360-45)°,
得18t-6t=180+360-45,解得t= ![]() 大于30,不合题意,
大于30,不合题意,
综上所述,当∠AOB=45°时,t=![]() 或
或![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案