题目内容
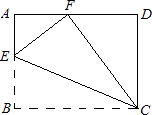
【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为 时,△ABE与以D、M、N为顶点的三角形相似.( ) 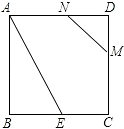
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
【答案】C
【解析】解:∵四边形ABCD是正方形, ∴AB=BC,
∵BE=CE,
∴AB=2BE,
又∵△ABE与以D、M、N为顶点的三角形相似,
∴①DM与AB是对应边时,DM=2DN
∴DM2+DN2=MN2=1
∴DM2+ ![]() DM2=1,
DM2=1,
解得DM= ![]() ;
;
②DM与BE是对应边时,DM= ![]() DN,
DN,
∴DM2+DN2=MN2=1,
即DM2+4DM2=1,
解得DM= ![]() .
.
∴DM为 ![]() 或
或 ![]() 时,△ABE与以D、M、N为顶点的三角形相似.
时,△ABE与以D、M、N为顶点的三角形相似.
故选C.
根据AE=EB,△ABE中,AB=2BE,所以在△MNC中,分CM与AB和BE是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目