Question

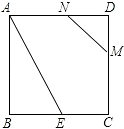
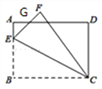
【题目】如图，矩形ABCD中，AB=6，BC=8，E为AB上一点，将△BCE沿CE翻折至△FCE，EF与AD相交于点G，且AG=FG，则线段AE的长为______．

Answer 1

【答案】

【解析】根据折叠的性质得到∠F=∠B=∠A=90°，BE=EF，根据全等三角形的性质得到FH=AE，GF=AG，得到AH=BE=EF，设AE=x，则AH=BE=EF=6-x，根据勾股定理即可得到结论．

∵将△CBE沿CE翻折至△CFE，

∴∠F=∠B=∠A=90°，BE=EF，

在△AGE与△FGH中，

，

∴△AGE≌△FGH，

∴FH=AE，GF=AG，

∴AH=BE=EF，

设AE=x，则AH=BE=EF=6-x，

∴DH=x+2，CH=8-x，

∵CD2+DH2=CH2，

∴62+（2+x）2=（8-x）2，

∴x=，

∴AE=，

故答案为：.