题目内容
【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点. 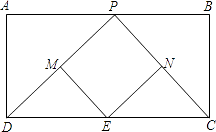
(1)求证:四边形PMEN是平行四边形;
(2)请直接写出当AP为何值时,四边形PMEN是菱形.
【答案】
(1)证明:∵M,E分别为PD,CD的中点,
∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形
(2)解:当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,
∴AP=BP,
在△APD和△BPC中,
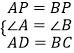 ,
,
∴△APD≌△BPC(SAS),
∴PD=PC,
∵M、N、E分别是PD、PC、CD的中点,
∴EN=PM= ![]() PD,PN=EM=
PD,PN=EM= ![]() PC,
PC,
∴PM=EM=EN=PN,
∴四边形PMEN是菱形
【解析】(1)由M、N、E分别是PD、PC、CD的中点,根据三角形中位线的性质,可证得ME∥PC,EN∥PD,继而证得四边形PMEN是平行四边形;(2)由AP=BP=5,可证得△APD≌△BPC(SAS),继而可得PD=PC,则可得PM=EM=EN=PN,继而证得四边形PMEN是菱形.
【考点精析】通过灵活运用平行四边形的判定和菱形的判定方法,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.

练习册系列答案
相关题目