题目内容
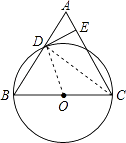
【题目】在等边△ABC中,以BC为直径的⊙O与AB交于点D,DE⊥AC,垂足为点E. 
(1)求证:DE为⊙O的切线;
(2)计算 ![]() .
.
【答案】
(1)证明:连接OD,
∵△ABC为等边三角形,
∴∠ABC=60°,
又∵OD=OB,
∴△OBD为等边三角形,
∴∠BOD=60°=∠ACB,
∴OD∥AC,
又∵DE⊥AC,
∴∠ODE=∠AED=90°,
∴DE为⊙O的切线
(2)解:连接CD,
∵BC为⊙O的直径,
∴∠BDC=90°,
又∵△ABC为等边三角形,
∴AD=BD= ![]() AB,
AB,
在Rt△AED中,∠A=60°,
∴∠ADE=30°,
∴AE= ![]() AD=
AD= ![]() AC,CE=AC﹣AE=
AC,CE=AC﹣AE= ![]() AC,
AC,
∴ ![]() =3.
=3.
【解析】(1)连接OD,根据等边三角形性质得出∠B=∠A=60°,求出等边三角形BDO,求出∠BDO,∠A,推出OD∥AC,推出OD⊥DE,根据切线的判定推出即可;(2)求出AD= ![]() AC,求出AE=
AC,求出AE= ![]() AC,CE=
AC,CE= ![]() AC,即可求出答案.
AC,即可求出答案.
【考点精析】本题主要考查了平行线的判定和等边三角形的性质的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目