题目内容
【题目】乘法公式的探究与应用：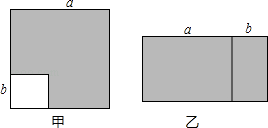
（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分面积是（写成两数平方差的形式）
（2）小颖将阴影部分裁下来，重新拼成一个长方形，如图乙，则长方形的长是 ， 宽是 ， 面积是（写成多项式乘法的形式）．
（3）比较甲乙两图阴影部分的面积，可以得到公式（用式子表达）
（4）运用你所得到的公式计算：10.3×9.7．
【答案】
（1）a2﹣b2
（2）a﹣b,a+b,（a+b）（a﹣b）
（3）a2﹣b2,a﹣b,a+b,（a+b）（a﹣b）,a2﹣b2
（4）解：10.3×9.7=（10+0.3）（10﹣0.3）
=102﹣0.32
=100﹣0.09
=99.91
【解析】解：（1）阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2；（2）长方形的宽为a﹣b，长为a+b，面积=长×宽=（a+b）（a﹣b）；（3）由（1）、（2）得到，（a+b）（a﹣b）=a2﹣b2；
（1）阴影部分的面积=大正方形的面积﹣小正方形的面积；（2）长方形的宽为a﹣b，长为a+b，面积=长×宽；（3）由（1）、（2）得到平方差公式.
练习册系列答案
阅读快车系列答案
相关题目
