题目内容
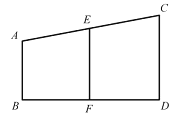
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
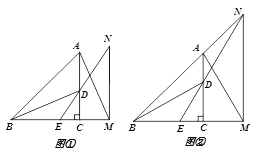
(2)如图①,若点E是BM的中点,求证:MN=AM;
(3)如图②,若点N落在BA的延长线上,求AM的长.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】分析:(1)、根据Rt△ACM的勾股定理得出AM的长度;(2)、①过点B作BF⊥BC与NE的延长线交于点F,首先证明△BEF≌△MEN,然后再证明Rt△BDC≌Rt△AMC,从而得出BD=AM,根据角平分线的性质以及平行线的性质得出∠BDF=∠F,从而得出答案;②过点D作DH⊥MN于点H,首先证明四边形CDHM是正方形,然后证明Rt△BDC≌Rt△AMC≌Rt△NDH,根据全等得出∠1=∠2=∠5=30°,根据Rt△BDC的三角函数得出答案.
详解:(1)![]() ;
;
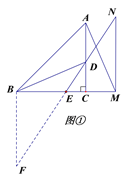
(2)证明:如图①,过点B作BF⊥BC与NE的延长线交于点F,
∵∠ACB=90°,MN∥AC,∴∠FBE=∠NME=90°, 又BE=ME,∠BEF=∠MEN,
∴△BEF≌△MEN,∴BF=MN, ∵CD=CM,BC=AC, ∴Rt△BDC≌Rt△AMC,∴BD=AM,
∵NF平分∠BDC,∴∠BDF=∠FDC, 又由BF∥AC,得:∠F=∠FDC,
∴∠BDF=∠F,∴BD=BF,∴MN=AM.
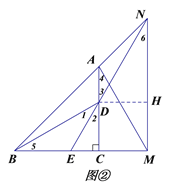
(3)如图②,过点D作DH⊥MN于点H,
∵MN∥AC,∠ACB=90°,CD=CM,∴四边形CDHM是正方形,
又点N在BA的延长线上,∴△BNM∽△BAC, ∵AC=BC,∴NM=BN,
又MH=CM=DH,∴NH=BC, ∴Rt△BDC≌Rt△AMC≌Rt△NDH, ∴BD=AM=ND,∠5=∠6,
又∠1=∠2,∠2=∠6,∴∠1=∠2=∠5, ∵∠1+∠2+∠5=90°,
∴∠1=∠2=∠5=30°, 在Rt△ABC中,AC=BC,AB=![]() ,∴AC=BC=4,
,∴AC=BC=4,
在Rt△BDC中,![]() ∴AM=
∴AM=![]() .
.

 阅读快车系列答案
阅读快车系列答案