题目内容
如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
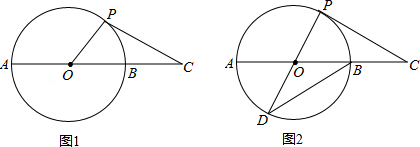
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
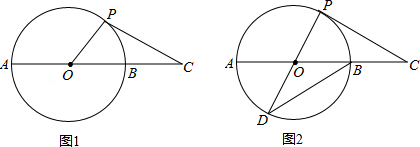
试题分析:(1)在△OPC中,底边OC长度固定,因此要想△OPC的面积最大,则要OC边上的高最大;由图形可知,当OP⊥OC时高最大;
(2)要想∠OCP的度数最大,由图形可知当PC与⊙O相切才能满足,根据切线的性质即可求得;
(3)连接AP,BP通过△ODB≌△BPC可求得DP⊥PC,从而求得PC是⊙O的切线
试题解析:(1)∵AB=4,
∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC=
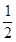 OC•h=2h,
OC•h=2h,∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
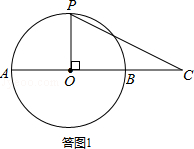
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.
(2)当PC与⊙O相切时,∠OCP最大.如答图2所示:

∵tan∠OCP=
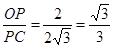 ,
,∴∠OCP=30°
∴∠OCP的最大度数为30°.
(3)证明:如答图3,连接AP,BP.
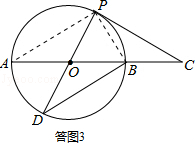
∴∠A=∠D=∠APD=∠ABD,
∵∠AOP=∠DOB
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD∠C,
在△ODB与△BPC中
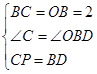 ,
,∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
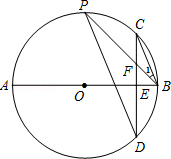
 ,求AE的长.
,求AE的长.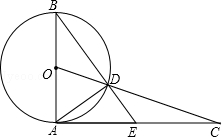
 BC;
BC;
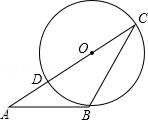
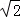 cm
cm