题目内容
【题目】如图，正比例函数y=x与反比例函数y=
的图象相交于A，C两点，AB⊥x轴于B，CD⊥x轴于D，则四边形ABCD的面积为 ．
【答案】2
【解析】
试题分析：首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|，得出S△AOB=S△ODC=，再根据反比例函数的对称性可知：OB=OD，得出S△ADB+S△BDC得出结果．
解：根据反比例函数的对称性可知：OB=OD，AB=CD，
∵四边形ABCD的面积等于S△ADB+S△BDC，
∵A（1，1），B（1，0），C（﹣1，﹣1），D（﹣1，0）
∴S△ADB=（DO+OB）×AB=×2×1=1，
S△BDC=（DO+OB）×DC=×2×1=1，
∴四边形ABCD的面积=2．
故答案为：2．
练习册系列答案
相关题目
【题目】某班在一次数学测验后成绩统计如下表：
分数段(分) | 40～49 | 50～59 | 60～69 | 70～79 | 80～89 | 90～100 |
人数 | 1 | 3 | 4 | 8 | 13 | 11 |
如果60分及以上为及格，那么这次数学测验的及格率是______．
【题目】某厂生产的RGZ-120型体重秤，最大称重120千克，你在体检时可看到如图（1）所示的显示盘。已知指针顺时针旋转角x（度）与体重y（千克）有如下关系：
x（度） | 0 | 72 | 144 | 216 |
y（千克） | 0 | 25 | 50 | 75 |
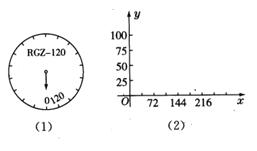
（1）根据表格中的数据在平面直角坐标系，图（2）中描出相应的点，顺次连接各点后，你发现这些点在哪一种函数的图象上？合情猜想符合这个图象的函数解析式；
（2）验证这些点的坐标是否满足函数解析式，归纳你的结论（写出自变量x的取值范围）；
（3）当指针旋转到158.4度的位置时，显示盘上的体重读数模糊不清，用解析式求出此时的体重。
