题目内容
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、EF,则
、EF,则![]() 的周长为
的周长为

A. 9B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
首先根据菱形的性质证明△ABE≌△ADF,然后连接AC可推出△ABC以及△ACD为等边三角形.根据等腰三角形三线合一的定理又可推出△AEF是等边三角形.根据勾股定理可求出AE的长,即可求出周长.
解:连接AC,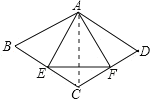
∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠B=∠D,∠B=180°-∠BCD=60°
∵E、F分别是BC、CD的中点,
∴BE=DF,
在△ABE和△ADF中,
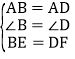
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF.
∵∠B=∠D=60°,
∴△ABC与△ACD是等边三角形,
∴AE⊥BC,AF⊥CD,
∴∠BAE=∠DAF=30°,
∴∠EAF=60°,
∴△AEF是等边三角形.
∵ AB=2,
∴AE=![]() ,
,
∴△AEF的周长是3![]() .
.
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
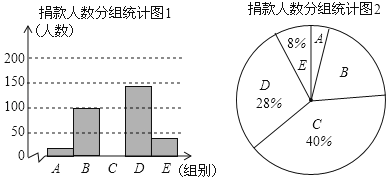
【题目】昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.