题目内容
将两个完全相同的长方形拼成如图所示的“L”形图案,判断△ACF是什么三角形?说明理由。

解:△ACF是等腰直角三角形 (1分)
∵两个长方形的大小完全相同 ∴ EF=DA ∠AEF=∠CDA=90° EA=DC
∴△AEF≌△CDA (SAS) (2分)
∴ AF=AC ∠EAF=∠DCA (3分)
又∵∠DCA+∠DAC=90°∴∠EAF+∠DAC=90°
即 ∠FAC=90° (4分)
∴△ACF为等腰直角三角形
∵两个长方形的大小完全相同 ∴ EF=DA ∠AEF=∠CDA=90° EA=DC
∴△AEF≌△CDA (SAS) (2分)
∴ AF=AC ∠EAF=∠DCA (3分)
又∵∠DCA+∠DAC=90°∴∠EAF+∠DAC=90°
即 ∠FAC=90° (4分)
∴△ACF为等腰直角三角形
根据题意可证△AEF≌△CDA,可得AF=AC,∠FAC=90°,从而得出△ACF为等腰直角三角形.
解:△ACF是等腰直角三角形.
∵两个长方形的大小完全相同
∴EF=DA,∠AEF=∠CDA=90°,EA=DC,
∴△AEF≌△CDA (SAS)
∴AF=AC,∠EAF=∠DCA,
又∵∠DCA+∠DAC=90°
∴∠EAF+∠DAC=90°
即∠FAC=90°
∴△ACF为等腰直角三角形.
解:△ACF是等腰直角三角形.
∵两个长方形的大小完全相同
∴EF=DA,∠AEF=∠CDA=90°,EA=DC,
∴△AEF≌△CDA (SAS)
∴AF=AC,∠EAF=∠DCA,
又∵∠DCA+∠DAC=90°
∴∠EAF+∠DAC=90°
即∠FAC=90°
∴△ACF为等腰直角三角形.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
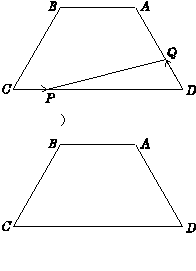





 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.

