题目内容
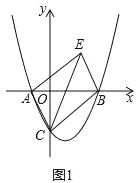
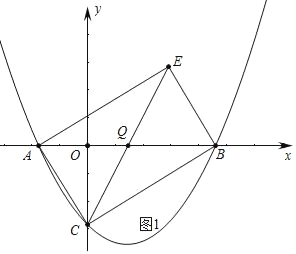
【题目】如图1,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.
与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.
(1)求∠BCE的度数;
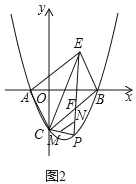
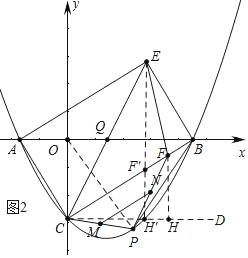
(2)如图2,F为线段BC上一动点,P为第四象限内抛物线上一点,连接CP、FP、BP、EF,M,N分别是线段CP,FP的中点,连接MN,当△BCP面积最大,且MN+EF最小时,求PF的长度;
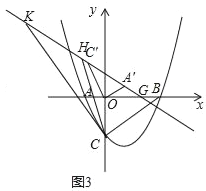
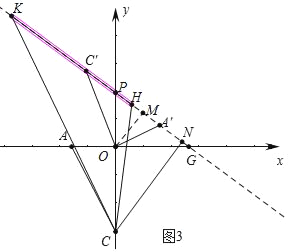
(3)如图3,将△AOC绕点O顺时针旋转一个角度α(0°<α<180°),点A,C的对应点分别为A',C',直线A'C'与x轴交于点G,G在x轴正半轴上且OG=![]() .线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.
.线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.
【答案】(1)30°;(2)PF=![]() ;(3)满足条件的点K的坐标为K(
;(3)满足条件的点K的坐标为K(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)在Rt△OBC中,tan∠OBC=![]() ,推出∠OBC=30°,由四边形ACBE是矩形,得出QB=QC,可得∠BCE=∠QBC=30°;
,推出∠OBC=30°,由四边形ACBE是矩形,得出QB=QC,可得∠BCE=∠QBC=30°;
(2)如图2中,作CD⊥y轴,FH⊥CD于H,EH′⊥CD于H′交BC于点F′,设P(m, ![]() ),根据S△PBC=S△POC+S△POB-S△OBC,构建二次函数,由重合时的性质确定点P的坐标,由CM=MP,FN=P,推出MN=
),根据S△PBC=S△POC+S△POB-S△OBC,构建二次函数,由重合时的性质确定点P的坐标,由CM=MP,FN=P,推出MN=![]() CF,在Rt△FCH中,易知∠FCH=30°,FH=
CF,在Rt△FCH中,易知∠FCH=30°,FH=![]() CF,得出FH=MN,进而得出MN+EF=EF+FH,从而知F与F′H与H′重合时,MN+EF的值最小,求出点F的坐标即可;
CF,得出FH=MN,进而得出MN+EF=EF+FH,从而知F与F′H与H′重合时,MN+EF的值最小,求出点F的坐标即可;
(3)如图3中,作OM⊥KH与M,直线KH交y轴于点P,作CN⊥KH于N,,确定直线KH的解析式,求出点N的坐标,分三种情况分别求解即可解决问题.
试题解析:(1)如图1中,设AB交CE于Q.
令y=0,得到![]() x2﹣
x2﹣![]() ﹣3=0,
﹣3=0,
解得x=﹣![]() 或3
或3![]() ,
,
∴A(﹣![]() ,0),B(3
,0),B(3![]() ,0),
,0),
在Rt△OBC中,tan∠OBC=![]() =
=![]() ,
,
∴∠OBC=30°,
∵四边形ACBE是矩形,
∴QB=QC,
∴∠BCE=∠QBC=30°.
(2)如图2中,作CD⊥y轴,FH⊥CD于H,EH′⊥CD于H′交BC于F′.
设P(m,![]() m2﹣
m2﹣![]() m﹣3),
m﹣3),
S△PBC=S△POC+S△POB﹣S△OBC=![]() ×3×m+
×3×m+![]() ×3
×3![]() ×(﹣
×(﹣![]() m2+
m2+![]() m+3)﹣
m+3)﹣![]() ×3×3
×3×3![]()
=﹣![]() m2+
m2+![]() m
m
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=![]() 时,△PBC的面积最大,此时P(
时,△PBC的面积最大,此时P(![]() ,﹣
,﹣![]() ),
),
∵CM=MP,FN=NP,
∴MN=![]() CF,
CF,
在Rt△FCH中,易知∠FCH=30°,
∴FH=![]() CF,
CF,
∴FH=MN,
∴MN+EF=EF+FH,
∴当F与F′重合,H与H′重合时,MN+EF的值最小.
易知E(2![]() ,3),F′(2
,3),F′(2![]() ,﹣1),
,﹣1),
∴PF=![]() =
=![]() .
.
(3)如图3中,作OM⊥KH于M,直线KH交y轴于P,作CN⊥KH于N.
在Rt△OMG中,易知,OM=![]() ,OM=
,OM=![]() ,
,
∴MG=![]() =2,
=2,
∵tan∠POG=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴OP=![]() ,
,
∴直线PG的解析式为y=﹣![]() x+
x+![]() ,
,
∵CN⊥PG,
∴直线CN的解析式为y=![]() x﹣3,
x﹣3,
由 ,解得
,解得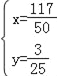 ,
,
∴N(![]() ,
,![]() ),
),
①当CK=CH时,NK=NH=![]() ,
,
点N向上平移![]() 个单位,向左平移2个单位得到K,
个单位,向左平移2个单位得到K,
∴K(![]() ,
,![]() ).
).
②当CK=KH时,设K(m,﹣![]() m+
m+![]() ),
),
∴m2+(﹣![]() m+
m+![]() +3)2=52,
+3)2=52,
解得m=![]() ,
,
∴K(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
③当CH=KH=5时,同法可得H(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
点H向上平移3个单位,向左平移4个单位得到K,
∴K(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
综上所述,满足条件的点K的坐标为K(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).