题目内容
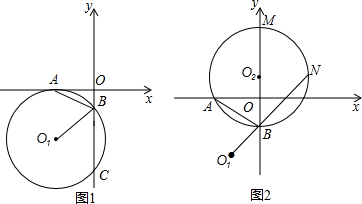
如图1,平面直角坐标系中,⊙O1与x轴相切于点A,与y轴相交于点B、C两点,连接AB、O1B.
(1)求证:∠ABO1=∠ABO;
(2)若点O1的坐标为(-
,-2),直接写出点B、C的坐标
(3)如图2,在(2)的条件下,过A、B两点作⊙O2与y轴的正半轴交于点M,与O1B的延长线交于点N,当⊙O2的大小变化时,给出下列两个结论:①BM-BN的值不变;②BM+BN的值不变;其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
(1)求证:∠ABO1=∠ABO;
(2)若点O1的坐标为(-
| 3 |
(3)如图2,在(2)的条件下,过A、B两点作⊙O2与y轴的正半轴交于点M,与O1B的延长线交于点N,当⊙O2的大小变化时,给出下列两个结论:①BM-BN的值不变;②BM+BN的值不变;其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.

分析:(1)连接O1A,由圆O1与x轴切于A,根据切线的性质得到O1A垂直于OA,由OB与AO垂直,根据平面内垂直于同一条直线的两直线平行,得到O1A与OB平行,根据两直线平行内错角相等,得到一对内错角相等,再由O1A=O1B,根据等边对等角可得出一对角相等,等量代换可得出∠ABO1=∠ABO,得证;
(2)作O1E⊥BC于点E,根据垂径定理得到E为BC的中点,由点O1的坐标为(-
,-2),可求得OE=O1B=O1A=2,O1E=OA=
,然后由勾股定理求得BE的长,继而求得OB与OC的长,则可求得点B、C的坐标;
(3)两个结论中,①BM-BN的值不变正确,理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,由∠ABO1为四边形ABMN的外角,根据圆内接四边形的外角等于它的内对角,可得出∠ABO1=∠NMA,再由∠ABO1=∠ABO,等量代换可得出∠ABO=∠NMA,然后利用同弧所对的圆周角相等可得出∠ABO=∠ANM,等量代换可得出∠NMA=∠ANM,根据等角对等边可得出AM=AN,再由同弧所对的圆周角相等,及OM=BN,利用SAS可得出三角形AMG与三角形ABN全等,根据全等三角形的对应边相等可得出AG=AB,由AO与BG垂直,根据三线合一得到O为BG的中点,根据OB的长求出BG的长,然后BM-BN=BM-MG=BG,由BG为常数得到BM-BN的长不变,得证.
(2)作O1E⊥BC于点E,根据垂径定理得到E为BC的中点,由点O1的坐标为(-
| 3 |
| 3 |
(3)两个结论中,①BM-BN的值不变正确,理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,由∠ABO1为四边形ABMN的外角,根据圆内接四边形的外角等于它的内对角,可得出∠ABO1=∠NMA,再由∠ABO1=∠ABO,等量代换可得出∠ABO=∠NMA,然后利用同弧所对的圆周角相等可得出∠ABO=∠ANM,等量代换可得出∠NMA=∠ANM,根据等角对等边可得出AM=AN,再由同弧所对的圆周角相等,及OM=BN,利用SAS可得出三角形AMG与三角形ABN全等,根据全等三角形的对应边相等可得出AG=AB,由AO与BG垂直,根据三线合一得到O为BG的中点,根据OB的长求出BG的长,然后BM-BN=BM-MG=BG,由BG为常数得到BM-BN的长不变,得证.
解答:解:(1)连接O1A,则O1A⊥OA,
又∵OB⊥OA,
∴O1A∥OB,
∴∠O1AB=∠ABO,
又∵O1A=O1B,
∴∠O1AB=∠O1BA,
∴∠ABO1=∠ABO;
(2)过点作O1E⊥BC于点E,
∴BE=CE,
∵点O1的坐标为(-
,-2),
∴OE=O1B=O1A=2,O1E=OA=
,
∴在Rt△BO1E中,BE=
=1,
∴OB=OE-BE=2-1=1,OC=OE+CE=2+1=3,
∴点B的坐标为:(0,-1),点C的坐标为:(0,-3);
 (3)①正确.
(3)①正确.
理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,
∵∠ABO1为四边形ABMN的外角,
∴∠ABO1=∠NMA,
又∵∠ABO1=∠ABO,
∴∠ABO=∠NMA,
又∵∠ABO=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN,
∵∠AMG和∠ANB都为
所对的圆周角,
∴∠AMG=∠ANB,
∵在△AMG和△ANB中,
,
∴△AMG≌△ANB(SAS),
∴AG=AB,
∵AO⊥BG,
∴BG=2BO=2,
∴BM-BN=BM-MG=BG=2其值不变.
又∵OB⊥OA,
∴O1A∥OB,
∴∠O1AB=∠ABO,
又∵O1A=O1B,
∴∠O1AB=∠O1BA,
∴∠ABO1=∠ABO;
(2)过点作O1E⊥BC于点E,
∴BE=CE,
∵点O1的坐标为(-
| 3 |
∴OE=O1B=O1A=2,O1E=OA=
| 3 |
∴在Rt△BO1E中,BE=
| O1B2-O1E2 |
∴OB=OE-BE=2-1=1,OC=OE+CE=2+1=3,
∴点B的坐标为:(0,-1),点C的坐标为:(0,-3);
 (3)①正确.
(3)①正确.理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,
∵∠ABO1为四边形ABMN的外角,
∴∠ABO1=∠NMA,
又∵∠ABO1=∠ABO,
∴∠ABO=∠NMA,
又∵∠ABO=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN,
∵∠AMG和∠ANB都为
 |
| AB |
∴∠AMG=∠ANB,
∵在△AMG和△ANB中,
|
∴△AMG≌△ANB(SAS),
∴AG=AB,
∵AO⊥BG,
∴BG=2BO=2,
∴BM-BN=BM-MG=BG=2其值不变.
点评:此题考查了切线的性质,坐标与图形性质,垂径定理,圆周角定理,勾股定理,等腰三角形的判定与性质,以及全等三角形的判定与性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=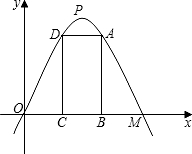 M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上.
M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上. ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP. 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为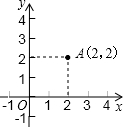 如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )
如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )