Question

【题目】如图1，在四边形ABCD中，AB⊥AD，AB⊥BC，以AB为直径的⊙O与CD相切于点E，连接OC、OD．

（1）求证：OC⊥OD；

（2）如图2，连接AC交OE于点M，若AB＝4，BC＝1，求的值．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）如图1中，连接OE．证明Rt△OCB≌Rt△OCE（HL），推出∠COB＝∠COE，同法可证：Rt△ODE≌Rt△ODA（HL），推出∠DOE＝∠DOA即可解决问题．

（2）作CH⊥AD于H，MK⊥AD于K，MJ⊥AB于J．设OM＝x．由题意DA，CD，BC是⊙O的切线，四边形ABCH是矩形，推出DE＝DA，CB＝CE＝1，设DE＝DA＝m，AH＝BC＝1，CH＝AB＝4，在Rt△CHD中，利用勾股定理求出m，再利用相似三角形的性质求出x，即可解决问题．

（1）证明：如图1中，连接OE．

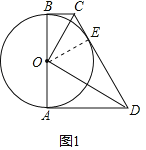
∵AB⊥BC，CD是⊙O的切线，

∴OE⊥CD，

∴∠OBC＝∠OEC＝90°，

∵OB＝OE，OC＝OC，

∴Rt△OCB≌Rt△OCE（HL），

∴∠COB＝∠COE，

同法可证：Rt△ODE≌Rt△ODA（HL），

∴∠DOE＝∠DOA，

∴∠DOC＝∠COE+∠DOE＝（∠BOE+∠EOC）＝90

∴OC⊥OD．

（2）解：作CH⊥AD于H，MK⊥AD于K，MJ⊥AB于J．设OM＝x．

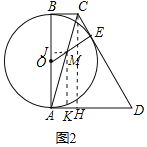
由题意DA，CD，BC是⊙O的切线，四边形ABCH是矩形，

∴DE＝DA，CB＝CE＝1，设DE＝DA＝m，AH＝BC＝1，CH＝AB＝4，

在Rt△CHD中，则有（m+1）2＝42+（m﹣1）2，

解得m＝4，

∴DH＝3，CD＝5，

∵∠MOJ+∠AOM＝180 ，∠D+∠AOM＝180 ，

∴∠MOJ＝∠D，

∵∠MJO＝∠CHD＝90 ，

∴△MJO∽△CHD，

∴＝＝，

∴＝＝，

∴OJ＝x，MJ＝x，

∵MJ∥BC，

∴AJ：AB＝MJ：BC，

∴（2+x）：4＝x：1，

解得x＝，

∴MJ＝，

∵MJ∥BC，

∴＝＝，

∴＝．