题目内容
【题目】如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.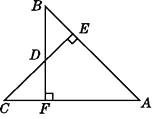
(1)求证:点D在∠BAC的平分线上.
(2)若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.
【答案】
(1)证明:∵CE⊥AB,BF⊥AC,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
∴DE=DF.
∴点D在∠BAC的平分线上.
(2)解:将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换仍然成立.理由如下:
∵CE⊥AB,BF⊥AC,
∴∠DEB=∠DFC=90°.
∵点D在∠BAC的平分线上,
∴DE=DF.
在△BDE与△CDF中,
∴△BDE≌△CDF(ASA).
∴BD=CD.
【解析】(1)根据垂直的定义得出∠DEB=∠DFC=90°.然后利用AAS判断出△BDE≌△CDF,根据全等三角形对应边相等得出DE=DF.根据角平分线的判定,到角两边距离相等的点在这个角的角平分线上得出点D在∠BAC的平分线上;
(2)将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换仍然成立.理由如下:根据垂直的定义得出∠DEB=∠DFC=90°.根据角平分线上的点到角两边的距离相等得出DE=DF,然后利用ASA判断出△BDE≌△CDF,根据全等三角形对应边相等得出BD=CD.
【考点精析】通过灵活运用角的平分线判定和角平分线的性质定理,掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目