Question

【题目】如图，在△ABD中，AB=AD，以AB为直径的⊙F交BD于点C，交AD于点E，CG⊥AD于点G，连接FE，FC．

（1）求证：GC是⊙F的切线；

（2）填空：

①若∠BAD=45°，AB=2，则△CDG的面积为_____．

②当∠GCD的度数为_____时，四边形EFCD是菱形．

Answer 1

【答案】 -； 30°．

【解析】（1）由等腰三角形的性质得出∠D=∠BCF，证出CF∥AD，由已知条件得出CG⊥CF，即可得出结论；

（2）解：①连接AC，BE，根据圆周角定理得到AC⊥BD，∠AEB=90°，根据等腰三角形的性质得到BC=CD，解直角三角形得到DE=2﹣2，根据三角形的中位线的性质得到DG=EG=DE=﹣1，CG=BE=1，于是得到结论；

②证出△BCF是等边三角形，得出∠B=60°，CF=BF=AB，证出△ABD是等边三角形，CF=AD，证出△AEF是等边三角形，得出AE=AF=AB=AD，因此CF=DE，证出四边形EFCD是平行四边形，即可得出结论．

（1）证明：∵AB=AD，FB=FC，

∴∠B=∠D，∠B=∠BCF，

∴∠D=∠BCF，

∴CF∥AD，

∵CG⊥AD，

∴CG⊥CF，

∴GC是⊙F的切线；

（2）解：①∵连接AC，BE，

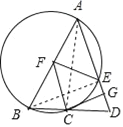
∵AB是⊙F的直径，

∴AC⊥BD，∠AEB=90°，

∵AB=AD，

∴BC=CD，

∵∠BAD=45°，AB=2，

∴BE=AE=2，

∴DE=2﹣2，

∵CG⊥AD，

∴CG∥BE，

∴DG=EG=DE=﹣1，CG=BE=1，

∴△CDG的面积=DGCG= ﹣；

故答案为： -；

∵CG⊥CF，∠GCD=30°，

∴∠FCB=60°，

∵FB=FC，

∴△BCF是等边三角形，

∴∠B=60°，CF=BF=AB，

∵AB=AD，

∴△ABD是等边三角形，CF=AD，

∴∠A=60°，

∵AF=EF，

∴△AEF是等边三角形，

∴AE=AF=AB=AD，

∴CF=DE，

又∵CF∥AD，

∴四边形EFCD是平行四边形，

∵CF=EF，

∴四边形EFCD是菱形；

故答案为：30°．