Question

【题目】如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为 ，上、下底之比为1：2，则BD的长是（ ）．

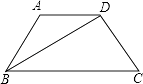
A.5
B.5
C.3
D.3

Answer 1

【答案】B
【解析】设梯形的四边长为5，5，x，2x， 则 , x=5， 则AB=CD=5，AD=5，BC=10， ∵AB=AD， ∴∠ABD=∠ADB， ∵AD∥BC， ∴∠ADB=∠DBC， ∴∠ABD=∠DBC， ∵∠ABC=60°， ∴∠DBC=30°， ∵等腰梯形ABCD，AB=DC， ∴∠C=∠ABC=60°， ∴∠BDC=90°， ∴在Rt△BDC中，由勾股定理得： ， 故答案为： ．根据题意设四边的长分别为5，5，x，2x，先根据平均数的公式求出四边的长，再证明△BDC是直角三角形，然后利用勾股定理求出BD的长即可。