题目内容
【题目】如图,已知OM、OA、ON是∠BOC内的三条射线,ON平分∠AOC,OM平分∠BOC,且∠AOB+∠MON=120°,则∠MON=______°.
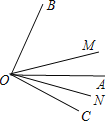
【答案】40
【解析】
设∠AOB=x°,∠MON=y°,先表示出∠BOC的度数,再根据角平分线的定义表示出∠MOC与∠NOC,然后根据∠MON=∠MOC-∠NOC列式整理得出规律,∠MON的度数等于∠AOB的一半,进行求解即可.
解:设∠AOB=x°,∠MON=y°,
则∠BOC=∠AOB+∠AOC=x°+∠AOC,
因为ON平分∠AOC,OM平分∠BOC.
所以∠MOC=![]() ∠BOC=
∠BOC=![]() +
+![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠AOC,
∠AOC,
所以∠MON=∠MOC-∠NOC=![]() x,
x,
即y=![]() x,
x,
由题意可得:x+![]() =120°,
=120°,
解得x=80°,
所以∠MON= y =40°.
故答案为:40

练习册系列答案
相关题目