Question

【题目】如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成长方形零件PQMN，使长方形PQMN的边QM在BC上，其余两个顶点P，N分别在AB，AC上，求这个长方形零件PQMN面积S的最大值．

Answer 1

【答案】这个长方形零件PQMN面积S的最大值是2400mm2

【解析】试题分析：设长方形零件PQMN的边PN=a，PQ=x，则AE=80﹣x，利用△APN∽△ABC得相似比，用相似比可得出用含x的式子表示a，故S=xa，从而得出二次函数解析式，根据解析式及自变量取值范围求S的最大值．

试题解析：设长方形零件PQMN的边PN=a，PQ=x，则AE=80﹣x． ∵PN∥BC，

∴△APN∽△ABC．

∴ = ．

因此， = ．

解得a=120﹣ x．

所以长方形PQMN的面积S=xa=x（120﹣ x）=﹣ x2+120x．

当x=﹣ 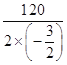=40时，a=60．

S最大值=40×60=2400（mm2）．

所以这个长方形零件PQMN面积S的最大值是2400mm2.