题目内容
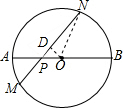
如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45゜.若AP=2,BP=6,求MN的长.


过点O作OD⊥MN于点D,连接ON,则MN=2DN,
∵AB是⊙O的直径,AP=2,BP=6,
∴⊙O的半径=
(2+6)=4,
∴OP=4-AP=4-2=2,
∵∠NPB=45゜,
∴△OPD是等腰直角三角形,
∴OD=
,
在Rt△ODN中,
DN=
=
=
,
∴MN=2DN=2
.
∵AB是⊙O的直径,AP=2,BP=6,
∴⊙O的半径=
| 1 |
| 2 |
∴OP=4-AP=4-2=2,
∵∠NPB=45゜,
∴△OPD是等腰直角三角形,
∴OD=
| 2 |
在Rt△ODN中,
DN=
| ON2-OD2 |
| 16-2 |
| 14 |
∴MN=2DN=2
| 14 |


练习册系列答案
相关题目