题目内容
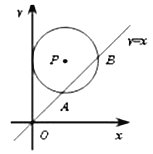
【题目】如图,在平面直角坐标系中,![]() 的圆心是
的圆心是![]() ,半径为3,函数
,半径为3,函数![]() 的图象被
的图象被![]() 的弦
的弦![]() 的长为
的长为![]() ,则a的值是( )
,则a的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
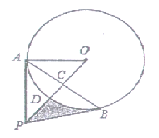
作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=3,PC=a,易得D点坐标为(3,3),则△OCD为等腰直角三角形,△PED也为等腰直角三角形.由PE⊥AB,根据垂径定理得AE=BE=![]() ,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=
,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=![]() ,所以a=3+
,所以a=3+![]() .
.
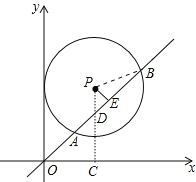
解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=![]() ,
,
在Rt△PBE中,PB=3,
∴PE=![]() ,
,
∴PD=![]() ,
,
∴a=![]() .
.
故答案为:D.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目